January 14, 2005

History of Weights and Measurements

By Dr. Frank J. Collazo

Introduction: The earliest weights seem to have been based on the objects being weighed, for example seeds and beans. Ancient measurements of length were based on the human body, for example the length of a foot, the length of a stride, the span of a hand, and the breadth of a thumb. There were unbelievably many different measurement systems developed in early times, most of them only being used in a small locality.

One which gained a certain universal nature was that of the Egyptian cubit developed around 3000 BC. Based on the human body, it was taken to be the length of an arm from the elbow to the extended fingertips. The report is organized in three sections. Section I provides the history of the weights and measurements in Babylonia, Egypt, Greece, Roman Empire, Europe, and the United States. Section 2 describes the evolution of the meter and secondly as a unit of measurement. Section 3 outlines the chronology of sequence events of the units of weights and measurements.

Egyptian Contribution: Since different people have different lengths of arm, the Egyptians developed a standard royal cubit, which was preserved in the form of a black granite rod against which everyone could standardize their own measuring rods. To measure smaller lengths required subdivisions of the royal cubit. Although we might think there is an inescapable logic in dividing it in a systematic manner, this ignores the way that measuring grew up with people measuring shorter lengths using other parts of the human body.

The digit was the smallest basic unit, being the breadth of a finger. There were 28 digits in a cubit, 4 digits in a palm, 5 digits in a hand, 3 palms (so 12 digits) in a small span, 14 digits (or a half cubit) in a large span, 24 digits in a small cubit, and several other similar measurements. Now one might want measurements smaller than a digit, and for this the Egyptians used measures composed of unit fractions.

Egyptian Papyri: It is not surprising that the earliest mathematics, which comes down to us, is concerned with problems about weights and measures, for this indeed must have been one of the earliest reasons to develop the subject. Egyptian papyri, for example, contain methods for solving equations, which arise from problems about weights and measures.

Babylonian Contribution: A later civilization whose weights and measures had a wide influence was that of the Babylonians around 1700 BC. Their basic unit of length was, like the Egyptians, the cubit. The Babylonian cubit (530 mm), however, was very slightly longer than the Egyptian cubit (524 mm). The Babylonian cubit was divided into 30 kus, which is interesting since the kus must have been about a finger's breadth, but the fraction ¹/₃₀ is one, which is also closely connected to the Babylonian base 60 number system. A Babylonian foot was ²/₃ of a Babylonian cubit. Now we commented in the previous paragraph about a subdivision of a Babylonian unit, which was closely related to their number system. This presents a problem as we look at developing systems of measures.

Many early number systems tended to be based on ten for the obvious reason that we have ten fingers on which to count. Most such systems were not positional systems, so the reason to use multiples of ten in measurement subdivision was less strong. Also ten is an unfortunate number into which to divide a unit of measurement since it only divides naturally into ¹/₂, ¹/₅, ¹/₁₀. Basing subdivisions on 12, mean that ¹/₂, ¹/₃, ¹/₄, ¹/₆, ¹/₁₂ are natural subdivisions, giving much more range for trading quantities. However, since most measuring systems seem to have grown up as a combination of different "natural" measures, no decision about a number to subdivide by would arise. One exception, and the earliest known decimal system of weights and measures, is the Harappan system.

Harappan System: The Harappan civilization flourished in the Punjab between 2500 BC and 1700 BC. The Harappans appear to have adopted a uniform system of weights and measures. An analysis of the weights discovered in excavations suggests that they had two different series, both decimal in nature, with each decimal number multiplied and divided by two. The main series has ratios of 0.05, 0.1, 0.2, 0.5, 1, 2, 5, 10, 20, 50, 100, 200, and 500. Several scales for the measurement of length were also discovered during excavations. One was a decimal scale based on a unit of measurement of 1.32 inches (3.35 centimeters), which has been called the "Indus inch". Of course ten units is then 13.2 inches (33.5 centimeters) which is quite believable as the measure of a "foot," although this suggests the Harappans had rather large feet!

Another scale was discovered when a bronze rod was found to have marks in lengths of 0.367 inches. It is certainly surprising the accuracy with which these scales are marked. Now 100 units of this measure are 36.7 inches (93 centimeters), which is about the length of a stride. Measurements of the ruins of the buildings that have been excavated show that the Harappans in their construction accurately used these units of length.

European System of Measurement: European systems of measurement were originally based on Roman measures, which in turn were based on those of Greece.

Greek Contribution: The Greeks used as their basic measure of length the breadth of a finger (about 19.3 mm), with 16 fingers in a foot, and 24 fingers in a Greek cubit. These units of length, as were the Greek units of weight and volume, were derived from the Egyptian and Babylonian units. Trade, of course, was the main reason why units of measurement were spread more widely than their local areas. In around 400 BC. Athens was a center of trade from a wide area. The Agora was the commercial center of the city, and we know from the plays of Aristophanes the type of noisy dealing that went on there. Most disputes would arise over the weights and measures of the goods being traded. Therefore, a standard set of measures was kept in order that such disputes might be settled fairly.

The size of a container to measure nuts, dates, beans, and other such items, had been laid down by law, and if a container was found which did not conform to the standard, its contents were confiscated and the container destroyed.

The Romans Adapted the Greek System: The Romans adapted the Greek system. They had as a basis the foot that was divided into 12 inches (or ounces for the words are in fact the same). The Romans did not use the cubit but, perhaps because most of the longer measurements were derived from marching, they had five feet equal to one pace (which was a double step that is the distance between two consecutive positions of where the right foot lands as one walks). The 1,000 paces measured a Roman mile, which is reasonably close to the British mile as used today. This Roman system was adopted, with local variations, throughout Europe as the Roman Empire spread. However, if one looks at a country like England, it was invaded at different times by many peoples bringing their own measures. The Angles, Saxons, and Jutes brought measures such as the perch, rod and furlong. The fathom has a Danish origin and was the distance from fingertip to fingertip of outstretched arms, while the ell was originally a German measure of woolen clothed.

British Contribution: In England and France measures developed in rather different ways. We have seen above how the problem of standardization of measures always presented problems, and in early 13^th century England a royal ordinance Assize of Weights and Measures gave a long list of definitions of measurement to be used. On one hand it was an extremely successfully attempt at standardization for its definitions lasted for nearly 600 years. The Act of Union between England and Scotland decreed that these standards would hold across the whole of Great Britain.

Locally, however, these standards were not always adhered to and districts still retained their own measures. Of course, although an attempt had been made to standardize measures, no attempt had been made to rationalize them and Great Britain retained a bewildering array of measures that were defined by the ordinance as rather strange subdivisions of each other. Scientists had long seen the benefits of rationalizing measures, and those such as Wren had proposed a new system based on the yard defined as the length of a pendulum beating at the rate of one second in the Tower of London.

France Contribution: In France, on the other hand, there was no standardization and as late as 1788 Arthur Young wrote in "Travels during the years 1787, 1788, 1789" published in 1793: “In France the infinite perplexity of the measures exceeds all comprehension. They differ not only in every province, but in every district and almost every town.”

In fact it has been estimated that France had about 800 different names for measures at this time, and taking into account their different values in different towns, around 250,000 differently sized units. To a certain extent this reflected the powers, which resided in the hands of local nobles who had resisted all attempts by the French King over centuries, to standardize measures. Some French scientists had proposed uniform systems at least 100 years before the French Revolution. Gabriel Mouton, in 1670, had suggested that the world should adopt a uniform scale of measurement based on the mille, which he defined as the length of one minute of the Earth's arc. He proposed that decimal subdivisions should be used to determine the lengths of shorter units of length.

Lalande, in April 1789, proposed that the measures used in Paris should become national ones, an attempt at standardization but not rationalization. This proposal was put to the National Assembly in February 1790, but in March a different suggestion was made. Talley Rand put to the National Assembly a proposal due to Condorcet, namely that a new measurement system be adopted based on a length from nature. The system should have decimal subdivisions; all measures of area, volume, weight etc should be linked to the fundamental unit of length. The basic length should be that of a pendulum, which beat at the rate of one second, was adopted. This proposal was not designed to bring in a French system of measurement but to design an international system of measurement, so agreement was sought from other countries.

An immediate problem was that the pendulum length depended on the latitude at which the experiment was performed so a latitude had to be chosen. The French proposed 45, which conveniently fell in France. The British proposed London, and the United States proposed the 38th parallel which was conveniently close to Thomas Jefferson's estate. Diplomatic wording allowed an international agreement to be reached, but in March 1791 Borda, as chairman of the Commission of Weights and Measures, proposed using instead of the length of a pendulum, the length of ¹/_10,000,000 of the distance from the pole to the equator of the Earth.

They might have obtained international agreement on this had they not declared that this distance would be determined by an accurate survey of the distance between Dunkerque and Barcelona. The Royal Society in London declared this was based on a measurement of France, the Americans were not prepared to accept the word of the French mathematicians for its length. and even in France it was claimed that the whole project was really proposed in order to gain information on the shape of the Earth. Indeed, probably Laplace and others were more interested in finding the shape of the Earth rather than the length of the meter.

Impact of the French Revolution: Delambre and Méchain measured the meridian from Dunkerque and Barcelona between 1792 and 1798. However between these dates the French Revolution progressed to the stage where the Académie des Sciences was abolished in August 1793, but before that Borda, Lagrange and Laplace had computed a provisional value for the meter based on the survey carried out by Cassini de Thury in 1740.

United States Approval: The National Assembly passed the metric system into law and a meter bar together with a kilogram weight was dispatched to the United States in the expectation that they would adopt the new measures. Congress hesitated because the standards were provisional. Britain became hostile to the meter, as did Germany, which wanted a standard based on the pendulum.

International Commission: An International Commission began work in September 1798 to replace the provisional values with precise ones computed from the data collected by Delambre and Méchain. By June of the following year the Commission had produced a platinum bar, which became the official definition of the meter, and in September 1799 the meter was required by law to be used in the Paris region. However, as one might expect, introducing the new measure was easier said than done. Part of the problem was that Greek and Latin prefixes like kilo- and centi- had been proposed to help make the new system internationally acceptable but were strongly disliked in France. It was also a law, which was essentially impossible to enforce, and, again as one might expect, many traders took the opportunity to cheat their customers. Teaching the metric system became compulsory in schools and the hope was that at least the next generation would accept it even if the current generation would not.

Napoleon Repeals the Standards: In November 1800 an attempt was made to make the system more acceptable by dropping the Greek and Latin prefixes and reinstating the older names for measures but with new metric values. In September of the following year it became illegal to use any other system of weights and measures anywhere in France, but it was largely ignored. It did not last long for, on 12 February 1812, Napoleon returned the country to its former units. The meter standard was still used in the sense that a fathom was declared to be 2 meters; there were 6 feet in a fathom and 12 inches in a foot.

Now, despite this retrograde move, Napoleon had a major effect on the spread of the metric system. French conquests of the Low Countries had seen the metric system introduced there and, on the defeat of Napoleon and the restoring of monarchy in those countries, they retained the system. The decimal metric system was passed into law in 1820.

Belgium Controversy: In 1830 Belgium became independent of Holland and made the metric system, together with its former Greek and Latin prefixes, the only legal measurement system. Perhaps the fact that the French had scrapped the system they invented helped its acceptance in other European countries. In 1840 the French government reintroduced the metric system but it took many years before use of the old measures died out.

British Empire Adoption of the Metric System: In the 1860s Britain, the United States and the German states all made moves towards adopting the metric system. It became legal in Britain in 1864 but a law, which was passed by the House of Commons to require its use throughout the British Empire, never made it through its final stages on to the statute books. Similarly in the United States it became legal in 1866, although its use was not made compulsory. The German states passed legislation in 1868, which meant that on the unification of these states to form Germany, use of the metric system was made compulsory.

British Opposition: It is interesting that many leading British scientists were opposed to the introduction of the metric system in Britain in 1864, which is one reason it only became legal but not compulsory. George Airy and John Herschel argued strongly against it, as did William Rankine who composed the poem The Three-Foot Rule:

Some talk of millimeters, and some of kilograms,
And some of deciliters, to measure beer and drams;
But I'm a British Workman, too old to go to school,
So by pounds I'll eat, and by quarts I'll drink, and I'll work by my three foot rule.

A party of astronomers went measuring the Earth,
And forty million meters they took to be its girth;
Five hundred million inches, though, go through from Pole to Pole;
So lets stick to inches, feet and yards, and the good old three foot rule.

International Conference: In 1870 the French in Paris convened an International Conference. Invitations had been sent to scientists from countries around the world with the aim of improving international scientific cooperation by having the metric system as the worldwide standard. War broke out between France and Prussia just before the delegates were due to arrive, however, and the German delegation did not attend. Wishing that any decision be a truly international one, the conference was postponed and met again in 1872. The outcome was the setting up of the International Bureau of Weights and Measures, to be situated in Paris, and the Convention of the Meter of 1875, which was signed by seventeen nations. Further countries signed up over the following years.

International Bureau of Weights and Measures: In 1889, the International Bureau of Weights and Measures replaced the original meter bar in Paris by a new one, and at the same time had copies of the bar sent to every country that had signed up to the Convention of the Meter. The definition now became the distance between two lines marked on a standard bar made from 90 percent platinum and 10 percent iridium. This remained the standard until 1960 when the International Bureau of Weights and Measures adopted a more accurate standard for international science when it defined the meter in terms of the wavelength of light emitted by the krypton-86 atom, namely 1,650,763.73 wavelengths of the orange-red line in the spectrum of the atom in a vacuum. The meter was redefined again in 1983, this time as the distance which light travels in a vacuum in ¹/_299,792,458 seconds. This remains the current definition. In all re-definitions, the length of the meter was always taken as close as possible to the value fixed in 1799 by data from the Delambre-Méchain survey.

Notice that the current definition defines the meter in terms of the second. Now Borda had argued against using the length of a pendulum, which beats at the rate of one second to define the meter in 1791 on the reasonable grounds that the second was not a fixed unit but could change with time. Indeed the second, then defined as 1/86,400 of the mean solar day, does change but the International Bureau of Weights and Measures introduced a fixed definition in 1956, as ¹/_{31,556,925.9747} of the length of the tropical year 1900. Although this fixed the value, it was seen as an unsatisfactory definition since the length of the year 1900 could never be measured after 1900.

It was changed in 1964 to 9,192,631,770 cycles of radiation associated with a particular change of state of the caesium-133 atom. By 1983 when the meter was defined in terms of the second, Borda's objection was no longer valid as the definition of the second by then did not have the astronomical definition, which was indeed variable.

Metric System: The Metric System, is a decimal system of physical units based on a unit of length known as the meter (Greek metron, “measure”). Introduced and adopted by law in France in the 1790s, a majority of countries subsequently adopted the metric system as a common system of weights and measures. Scientists in all countries use the metric system in their work.

The meter (m), which is approximately 39.37 in, was originally defined as one ten-millionth of the distance from the equator to the North Pole on a line running through Paris. From 1792 to 1799, French scientists measured part of this distance. Treating the Earth as a perfect sphere, they then estimated the total distance and divided it into ten-millionths. Later, after it was discovered that the Earth is not a perfect sphere, the standard meter was defined as the distance between two fine lines marked on a bar of platinum-iridium alloy. In 1960 the meter was redefined as 1,650,763.73 wavelengths of the reddish-orange light given off by a form of the element krypton. The measurements of modern science required still greater precision; however, and in 1983 the meter was defined as the length of the path traveled by light in a vacuum during a time interval of 1/299,792,458 of a second.

The United States uses inches, feet, miles, pounds, tons, and gallons as units of length, weight, and volume for common measurements. Today, however, within the framework of the International System of Units, these English-system units are legally based on metric standards.

Using the Metric System: The metric system is known for its simplicity. All units of measurement in the metric system are based on decimals—that is, units that increase or decrease by multiples of ten. A series of Greek decimal prefixes is used to express units of ten or greater; a similar series of Latin decimal prefixes is used to express fractions. For example, deca equals ten, hecto equals one hundred, kilo equals one thousand, mega equals one million, giga equals one billion, and tera equals one trillion. For units below one, deci equals one-tenth, centi equals one-hundredth, milli equals one-thousandth, micro equals one-millionth, nano equals one-billionth, and pico equals one-trillionth. For conversion of metric system units to English-system units, see Weights and Measures.

Length: People who were taught the English system of measurements in schools in the United States often have difficulty visualizing metric units. One way to visualize a meter is to think of the distance from the floor to the top of a doorknob, or the distance from the edge of an adult’s shoulder to the end of the opposite outstretched arm. Smaller things are measured in centimeters and millimeters. A millimeter is quite small, about the thickness of a dime.

A centimeter is ten times bigger, about the height of a stack of ten dimes. Thereafter meters are used until one reaches distances about the length of five city blocks when kilometers are used. One kilometer is the approximate distance that an adult can walk in 12 minutes in a straight line and on a level road. Kilometers are used to measure long distances within cities or between cities.

Volume: Small volumes, such as the contents of a drinking glass, are measured in cubic centimeters, and large volumes, such as the contents of industrial fuel tanks, are measured in liters. A liter is 1,000 cubic centimeters—also known as 1,000 milliliters. Strictly speaking a cubic centimeter and a milliliter are not exactly the same. However, the difference is so slight that it may be ignored for everyday use.

Weight: Small volumes, such as the contents of a drinking glass, are measured in cubic centimeters, and large volumes, such as the contents of industrial fuel tanks, are measured in liters. A liter is 1,000 cubic centimeters—also known as 1,000 milliliters. Strictly speaking a cubic centimeter and a milliliter are not exactly the same. However, the difference is so slight that it may be ignored for everyday use. A normal-sized drinking glass contains about 300 milliliters. The size of a liter is increasingly well known in the United States because of the many one-liter beverage bottles found in grocery stores or supermarkets. Very large volumes are measured in cubic meters. Freight containers used in the shipping industry, including railroad, truck, and ocean shipping, have a capacity of about 70 cubic meters.

The basic unit of weight in the metric system is called a gram, and it is equal to the weight of one cubic centimeter of water. This is a very small amount, but it is easy to comprehend. Just pick up a U.S. dollar bill (or any bank note), and its weight is one gram. Because the gram is too light to be a convenient standard of weight, a larger unit has been chosen. This unit is 1,000 grams. Following the regular pattern of metric naming, it is called one kilogram. One thousand grams of water occupy a volume of 1,000 cubic centimeters or one liter. Therefore, a person need only pick up a plastic one-liter bottle of water to understand how heavy a kilogram is. Very heavy objects are weighed in tons of 1,000 kilograms each. One thousand kilograms is equal to one metric ton and is not the same as the usual American ton of 907.2 kg.

Adoption of the Metric System: In the United States several attempts were made to bring the metric system into general use. In 1821 Secretary of State John Quincy Adams, in a report to Congress, advocated the adoption of the metric system. In 1866 Congress legalized the use of the metric system, and the system was increasingly adopted, notably in medicine and science, as well as in certain sports, such as track and field. In 1893 the Office of Weights and Measures (now the National Institute of Standards and Technology) of the United States adopted the metric system in legally defining the yard and the pound.

In 1965 the United Kingdom became the first of the English-speaking countries to begin an organized effort to abandon the older units of measurement. Canada, Australia, New Zealand, and South Africa quickly followed and adopted the changeover more rapidly than the United Kingdom.

In 1971, after an extensive study, the U.S. secretary of commerce recommended that the United States convert to metric units under a ten-year voluntary plan. In 1975 President Gerald R. Ford signed the Metric Conversion Act. It defines the metric system as being the International System of Units as interpreted in the United States by the secretary of commerce. The act called for voluntary adoption of the metric system. In 1988 a provision in new federal legislation called for all federal agencies to use the metric system in business transactions starting in 1992, but this was never implemented. Lack of public interest and support has prevented the metric system from being adopted in the United States.

Summary: Ancient measurement of length was based on the human body, for example the length of a foot, the length of a stride, the span of a hand, and the breadth of a thumb. The Egyptian cubit was developed around 3000 BC. The Egyptians developed a standard royal cubit, which was preserved in the form of a black granite rod against which everyone could standardize their own measuring rods. A later civilization whose weights and measures had a wide influence was that of the Babylonians around 1700 BC.

The Harappans appear to have adopted a uniform system of weights and measures with two options. One was a decimal scale based on a unit of measurement of 1.32 inches (3.35 centimeters), which has been called the "Indus inch." The Harappans had rather large feet! Another scale was discovered when a bronze rod was found to have marks in lengths of 0.367 inches. Now 100 units of this measure are 36.7 inches (93 centimeters), which is about the length of a stride.

European systems of measurement were originally based on Roman measures, which in turn were based on those of Greece. The Greeks used as their basic measure of length the breadth of a finger (about 19.3 mm), with 16 fingers in a foot, and 24 fingers in a Greek cubit. Athens was a center of trade from a wide area. The Romans adapted the Greek system. Then 1,000 paces measured a Roman mile, which is reasonably close to the British mile as used today. The fathom has a Danish origin, and was the distance from fingertip to fingertip of outstretched arms.

The Act of Union between England and Scotland decreed that these standards would hold across the whole of Great Britain. British Scientists proposed a new system based on the yard defined as the length of a pendulum beating at the rate of one second in the Tower of London. The basic length of a pendulum, which beat at the rate of one second, was adopted. Britain and Germany became hostile to the meter, which wanted a standard based on the pendulum. In 1830, Belgium became independent of Holland and made the metric system, together with its former Greek and Latin prefixes, the only legal measurement system.

The Metric System was adopted in Britain 1864. In 1866, the system became legal in the United States, although its use was not made compulsory. The German states passed legislation in 1868 to adopt the Metric System. In 1889, the International Bureau of Weights and Measures replaced the original meter bar in Paris by a new one and at the same time had copies of the bar sent to every country which had signed up to the Convention of the Meter. Note that in all these redefinitions, the length of the meter was always taken as close as possible to the value fixed in 1799 by data from the Delambre-Méchain survey.

The current definition defines the meter in terms of the second. In 1866 Congress legalized the use of the metric system, and the system was increasingly adopted, notably in medicine and science, as well as in certain sports, such as track and field. In 1893 the Office of Weights and Measures (now the National Institute of Standards and Technology) of the United States adopted the metric system in legally defining the yard and the pound. In 1965 the United Kingdom became the first of the English-speaking countries to begin an organized effort to abandon the older units of measurement. In 1971, after an extensive study, the U.S. secretary of commerce recommended that the United States convert to metric units under a ten-year voluntary plan. In 1975 President Gerald R. Ford signed the Metric Conversion Act.

Evolution of Weights and Measurements

Introduction: The purpose of this section is to outline the definitions of the second and the meter as influenced by the Egyptians, Babylonians, Greeks, British, Danish, French, and the International Community:

Egyptian Concept (3000 BC): The Egyptians developed a standard royal cubit, which was preserved in the form of a black granite rod against which everyone could standardize their own measuring rods.

There were 28 digits in a cubit, 4 digits in a palm, 5 digits in a hand, 3 palms (so 12 digits) in a small span, 14 digits (or a half cubit) in a large span, 24 digits in a small cubit, and several other similar measurements:

28 digits = one cubit

24 digit = small cubit

14 digits = large span

12 digits or 3 palms = small span

4 digits = one palm

5 digits = one hand

Babylonian Concept (2500-1700):

Babylonian cubit = 530 mm = 30 kus

Babylonian foot = 2/3 Babylonian cubit

Kus = finger breadth (1/30)

Egyptian cubit = 524 mm

Harappan System (2500-1700):

Indus Inch = 1.32 inches = 3.35 cm

Foot = 13..32 inches

36.7 inches (93 centimeters) = length of a stride.

Greek Concept (400 BC):

Foot = 16 fingers

Finger Breadth = 19.3 mm (Greek)

Greek Cubit = 24 finger breath

Romans Adopted the Greek System:

1 foot = 12 inches

Roman Mile = 1000 paces

Danish Concept (400-BC):

The fathom has a Danish origin and was the distance from fingertip to fingertip of outstretched arms while the ell was originally a German measure of woolen clothed.

Fathom = the distance from fingertip to fingertip of outstretched arms.

Fathom = 2 meters, 6 ft in one fathom, and 12 inches in a foot.

British Concept (13th Century):

Definition of the second = the length of a pendulum beating at the rate of one second in the Tower of London.

One second = Instead of the length of a pendulum, the length of 1/10,000,000 of the distance from the pole to the equator of the Earth.

France Concept (1670-1800):

Mille = he defined as the length of one minute of the Earth's arc.

Second = the basic length should be that of a pendulum which beat at the rate of one second.

Redefinition of the second = Indeed the second, then defined as 1/86,400 of the mean solar day.

Redefinition of the second = British Scientists proposed using instead of the length of a pendulum, the length of 1/10,000,000 of the distance from the pole to the equator of the Earth.

Platinum Bar = A platinum bar which became the official definition of the meter.

Redefinition of the Fathom: The meter standard was still used in the sense that a fathom was declared to be 2 meters; there were 6 feet in a fathom and 12 inches in a foot.

The original meter bar definition was replaced by the distance between two lines marked on a standard bar made from 90 percent platinum and 10 percent iridium.

Meter Bar defined = Became the distance between two lines marked on a standard bar made from 90 percent platinum and 10 percent iridium.

International Standards:

Redefinition of the Meter (1960) = The meter was re-defined in terms of the wavelength of light emitted by the krypton-86 atom, namely 1,650,763.73 wavelengths of the orange-red line in the spectrum of the atom in a vacuum.

Redefinition of the meter (1956) = as 1/31,556,925.9747 of the length of the tropical year 1900. Although this fixed the value, it was seen as an unsatisfactory definition since the length of the year 1900 could never be measured after 1900.

Redefinition of the meter (1964) = It was changed in 1964 to 9,192,631,770 cycles of radiation associated with a particular change of state of the caesium-133 atom.

Redefining of the meter (1983) = as the distance which light travels in a vacuum in 1/299,792,458 seconds.

Metric Weights and Measures: A millimicron is one thousandth of one millionth of one meter. Most of the world uses the metric system. The only countries not on this system are the U.S., Myanmar, and Liberia. The metric system is based on 10s. For example, 10 decimeters make a meter (39.37 inches).

Units smaller than a meter have Latin prefixes:

Deci- means 10; 10 decimeters make a meter.
Centi- means 100; 100 centimeters make a meter.
Milli- means 1,000; 1,000 millimeters make a meter.

Units larger than a meter have Greek prefixes:

Deka means 10; a dekameter is 10 meters.
Hecto- means 100; a hectometer is 100 meters.
Kilo- means 1,000; a kilometer is 1,000 meters.

The International System (Metric)

Source: Department of Commerce, National Bureau of Standards. The International System of Units is a modernized version of the metric system, established by international agreement that provides a logical and interconnected framework for all measurements in science, industry, and commerce. The system is built on a foundation of seven basic units, and all other units are derived from them. (Use of metric weights and measures was legalized in the United States in 1866, and our customary units of weights and measures are defined in terms of the meter and kilogram.)

Length (Meter): Up until 1983, the meter was defined as 1,650,763.73 wavelengths in a vacuum of the orange-red line of the spectrum of krypton-86. Since then, it is equal to the distance traveled by light in a vacuum in 1/299,792,45 of a second.

Time (Second): The second is defined as the duration of 9,192,631,770 cycles of the radiation associated with a specified transition of the cesium-133 atom.

Mass (Kilogram): The standard for the kilogram is a cylinder of platinum-iridium alloy kept by the International Bureau of Weights and Measures at Paris. A duplicate at the National Bureau of Standards serves as the mass standard for the United States. The kilogram is the only base unit still defined by a physical object.

Temperature (Kelvin): The kelvin is defined as the fraction 1/273.16 of the thermodynamic temperature of the triple point of water; that is, the point at which water forms an interface of solid, liquid, and vapor. This is defined as 0.01°C on the Centigrade or Celsius scale and 32.02°F on the Fahrenheit scale. The temperature 0 K is called “absolute zero.”

Electric Current (Ampere): The ampere is defined as that current that, if maintained in each of two long parallel wires separated by one meter in free space, would produce a force between the two wires (due to their magnetic fields) of 2 × 10-7 Newton for each meter of length. (A newton is the unit of force that when applied to one kilogram mass would experience an acceleration of one meter per second per second.)

Luminous Intensity (Candela): The candela is defined as the luminous intensity of 1/600,000 of a square meter of a cavity at the temperature of freezing platinum (2,042°K).

Amount of Substance (Mole): The mole is the amount of substance of a system that contains as many elementary entities as there are atoms in 0.012 kilogram of carbon-12.

Zero on the Fahrenheit scale represents the temperature produced by the mixing of equal weights of snow and common salt.

	°Fahrenheit	°Celsius
Boiling point of water	212°	100°
Freezing point of water	32°	0°
Absolute zero	273.1°	459.6°

Absolute zero is theoretically the lowest possible temperature, the point at which all molecular motion would cease.

Measuring Motion: Speed is the measure of motion. You can find it by dividing the distance covered by the time it takes to travel that distance.

Speed of Light: If a star is 10 light-years away, it is about 60 trillion miles distant. Light travels through space at 186,000 miles per second.

Light-Year: A light ray travels 5.88 trillion miles a year in space.

Star Distance: The star Sirius is 9 light-years away from the solar system.

More Earthly Speeds:

Cheetah: 70 mph
White-tailed deer: 32 mph
Human being: 27.89 mph
Garden snail: 0.03 mph
Fastest automobile: 205 mph
Fastest train: 252 mph
Fastest helicopter: 249.10 mph
Fastest jet: 2,193.167 mph

Horsepower: A workhorse can lift 550 pounds 1 foot in the air in 1 second; that is 1 horsepower. Engines are measured in horsepower. A 10-horsepower engine can do the work of ten horses.

Manpower: An average man lifts 55 pounds 1 foot high in 1 second.

Candlepower: The amount of light given off by a candle of a specific size, shape, type of tallow, and type of wick. The brightness of an electric light is measured in candlepower.

Megaton: A megaton is the blasting power of a hydrogen bomb. One megaton has the power of 1 million tons of TNT.

Nautical Measurement:

A fathom is 6 feet, the length of rope a man can extend from open arm to open arm. The rope was lowered into the sea to measure depth.

A cable length is the length of a ship's cable, about 600 feet. A nautical mile is 10 cable lengths, or 6,076 feet.

1 nautical mile = 1.1508 miles

A knot is the measure of speed on water. One knot is 1 nautical mile per hour.

How Early Measures Made Their Mark: Dividing things into units is an ancient task. Here are four basic units and the people who first used them. You will recognize how they are still used today.

Binary: This Hindu unit divides things into halves, quarters, and eights. Modern computer programs are based on binary code.

Decimal: The Chinese and the Egyptians were the first to use decimals, which are tenths. The metric system is based on decimal units. The decimal system of writing numbers was introduced into Europe in the 1300s and is now widely used.

Duodecimal: The Romans used units of 12. Today we have 12 inches in a foot, 12 months in a year, 12 in a dozen.

Sexagesimal: The Babylonians used units of 60. Time is measured in 60s: 60 seconds in a minute, 60 minutes in an hour.

Miscellaneous Units of Measure:

Acre = An area is 43,560 square feet. Originally, it was the area a yoke of oxen could plow in one day.

Agate = Originally a measurement of type size (51/2 points), now equal to 1/14 inch. Used in printing for measuring column length.

Ampere = Unit of electric current. A potential difference of one volt across a resistance of one ohm produces a current of one ampere.

Astronomical Unit (A.U.) = 93,000,000 miles, the average distance of the earth from the sun. Used for astronomy.

Bale = A large bundle of goods. In the U.S., the approximate weight of a bale of cotton is 500 pounds. The weight varies in other countries.

Board Foot (fbm) = 144 cubic inches (12 in. × 12 in. × 1 in.). Used for lumber.

Bolt = 40 yards. Used for measuring cloth.

Btu = British thermal unit. Amount of heat needed to increase the temperature of one pound of water by one degree Fahrenheit (252 calories).

Carat (c) = 200 milligrams or 3.086 grains troy. Originally the weight of a seed of the carob tree in the Mediterranean region. Used for weighing precious stones.

Chain (ch) = A chain 66 feet or one-tenth of a furlong in length, divided into 100 parts called links. One mile is equal to 80 chains. Used in surveying and sometimes called Gunter's or Surveyor's chain.

Cubit = 18 inches or 45.72 cm. Derived from distance between elbow and tip of middle finger.

Decibel = Unit of relative loudness. One decibel is the smallest amount of change detectable by the human ear.

Ell, English = 11/4 yards or 1/32 bolt. Used for measuring cloth.

Freight = Ton (also called measurement ton).

40 Cubic Feet of Merchandise = Used for cargo freight.

Great Gross = 12 gross or 1728.

Gross = 12 dozen or 144.

Hand = 4 inches or 10.16 cm. Derived from the width of the hand. Used for measuring the height of horses at withers.

Hertz = Modern unit for measurement of electromagnetic wave frequencies (equivalent to “cycles per second”).

Hogshead (hhd) = Liquid barrels or 14,653 cubic inches.

Horsepower = The power needed to lift 33,000 pounds a distance of one foot in one minute (about 11/2 times the power an average horse can exert). Used for measuring power of steam engines, etc.

Karat (kt) = A measure of the purity of gold, indicating how many parts out of 24 are pure. For example: 18-karat gold is 3/4 pure. Sometimes spelled carat.

Knot = Not a distance but the rate of speed of one nautical mile per hour. Used for measuring speed of ships.

League = Rather indefinite and varying measure, but usually estimated at 3 miles in English speaking countries.

Light Year = 5,880,000,000,000 miles, the distance light travels in a vacuum in a year at the rate of 186,281.7 miles (299,792 kilometers) per second. (If an astronomical unit were represented by one inch, a light-year would be represented by about one mile.) Used for measurements in interstellar space.

Magnum = Two-quart bottle. Used for measuring wine, etc.

Ohm = Unit of electrical resistance. A circuit in which a potential difference of one volt produces a current of one ampere has a resistance of one ohm.

Parsec = Approximately 3.26 light-years or 3.08 × 1013 km (1.92 × 1013 mi). Term is combination of first syllables of parallax and second, and distance is that of imaginary star when lines drawn from it to both Earth and the Sun form a maximum angle or parallax of one second (1/3600 degree). Used for measuring interstellar distances.

pi (p)=3.14159265+. The ratio of the circumference of a circle to its diameter. For practical purposes, the value is used to four decimal places: 3.1416.

Pica = 1/6 inch or 12 points. Used in printing for measuring column width, etc.

Pipe = 2 hogsheads. Used for measuring wine and other liquids.

Point = .013837 (approximately 1/72) inch or 1/12 pica. Used in printing for measuring type size.

Quintal = 100,000 grams or 220.46 pounds avoirdupois.

Quire = Used for measuring paper. Sometimes 24 sheets but more often 25. There are 20 quires to a ream.

Ream = Used for measuring paper. Sometimes 480 sheets, but more often 500 sheets.

Roentgen = International Unit of radiation exposure produced by X-rays.

Score = 20 units.

Sound, Speed of = Usually placed at 1,088 ft. per second at 32°F at sea level. It varies at other temperatures and in different media.

Span = 9 inches or 22.86 cm. Derived from the distance between the end of the thumb and the end of the little finger when both are outstretched.

Square = 100 square feet. Used in building.

Stone = Legally 14 pounds avoirdupois in the U.K.

Therm = 100,000 btu's.

Township = U.S. land measurement of almost 36 square miles. The south border is 6 miles long. The east and west borders, also 6 miles long, follow the meridians, making the north border slightly less than 6 miles long. Used in surveying.

Tun = 252 gallons, but often larger. Used for measuring wine and other liquids.

Watt = Unit of power. The power used by a current of one ampere across a potential difference of one volt equals one watt.

Origins of Measurements: In ancient times, the body ruled when it came to measuring. The length of a foot, the width of a finger, and the distance of a step were all accepted measurements.

Inch = At first an inch was the width of a man's thumb. In the 14th century, King Edward II of England ruled that 1 inch equal 3 grains of barley placed end to end lengthwise.

Hand = A hand was approximately 5 inches or 5 digits (fingers) across. Today, a hand is 4 inches and is used to measure horses (from the ground to the horse's withers, or shoulder).

Span = A span was the length of the hand stretched out, about 9 inches.

Foot = In ancient times, the foot was 111/42 inches. Today it is 12 inches, the length of the average man's foot.

Yard = A yard was originally the length of a man's belt or girdle, as it was called. In the 12th century, King Henry I of England fixed the yard as the distance from his nose to the thumb of his out-stretched arm. Today it is 36 inches, about the distance from nose to out-stretched arm of a man.

Cubit = In ancient Egypt, a cubit was the distance from the elbow to the fingertips. Today a cubit is 18 inches.

Lick = A Lick was used by the Greeks to measure the distance from the tip of the thumb to the tip of the index finger.

Pace = The ancient Roman soldiers marched in paces, which were the length of a double step, about 5 feet; 1,000 paces was a mile. Today, a pace is the length of one step, 21/2 to 3 feet.

Measurements:

Inch = 0.083 feet
Foot = 12 inches
Yard = 3 feet or 36 inches
Mile = 5,280 feet or 1,760 yards

Near and Far:

Around the earth (at the equator): 24,901 miles
Across the continental U.S.: 3,000 miles
From the earth to the moon: 238,854 miles
From the earth to the sun: 93,000,000 miles

Cooking Measurement Equivalents (see the Infoplease.com conversion calculator):

1 tablespoon (tbsp) = 3 teaspoons (tsp)

1/16 cup = 1 tablespoon

1/8 cup = 2 tablespoons

1/6 cup = 2 tablespoons + 2 teaspoons

1/4 cup = 4 tablespoons

1/3 cup = 5 tablespoons + 1 teaspoon

3/8 cup = 6 tablespoons

1/2 cup = 8 tablespoons

2/3 cup = 10 tablespoons + 2 teaspoons

3/4 cup = 12 tablespoons

1 cup = 48 teaspoons

1 cup = 16 tablespoons

8 fluid ounces (fl oz) = 1 cup

1 pint (pt) = 2 cups

1 quart (qt) = 2 pints

4 cups = 1 quart

1 gallon (gal) = 4 quarts

16 ounces (oz) = 1 pound (lb)

1 milliliter (ml) = 1 cubic centimeter (cc)

1 inch (in) = 2.54 centimeters (cm)

Source: United States Dept. of Agriculture (USDA)

U.S. and Metric Cooking Conversions:

US to Metric:

Capacity Weight

1/5 teaspoon 1 milliliter 1 ounce 28 grams

1 teaspoon 5 ml 1 pound 454 grams

1 tablespoon 15 ml

1 fluid oz 30 ml

1/5 cup 47 ml

1 cup 237 ml

2 cups (1 pint) 473 ml

4 cups (1 quart) .95 liter

4 quarts (1 gallon) 3.8 liters

91 gallon

Metric to US:

Capacity Weight

1 milliliter 1/5 teaspoon 1 gram .035 ounce

5 ml teaspoon 100 grams 3.5 ounces

15 ml 1 tablespoon 500 grams 1.10 pounds

100 ml 3.4 fluid oz 1 kilogram 2.205 pounds

240 ml 1 cup 35 ounce

1 liter 34 fluid oz, 4.2 cups, 2.1 pints, 1.06 quarts, 0.26 gallon

Linear Measure:

12 inches (in.) = 1 foot

3 feet = 1 yard

51/2 yards = 1 rod, pole, or perch (161/2 ft.)

40 rods = 1 furlong (fur) = 220 yds = 660 ft.

8 furlongs = 1 statute mile (mi.) = 1,760 yds = 5,280 ft

3 land miles = 1 league

5,280 feet = 1 statute or land mile

6,076.11549 feet = 1 international nautical mile

Area Measure:

144 square inches = 1 sq ft.

9 square feet =1 sq yd = 1,296 sq in.

301/4 square yards = 1 sq rd = 2721/4 sq ft.

160 square rods = 1 acre = 4,840 sq yds = 43,560 sq ft.

640 acres = 1 sq. mi.

1 mile square = 1 section (of land)

6 miles square =1 township = 36 sections = 36 sq mi.

Gunter's or Surveyor's Chain Measure:

7.92 inches = 1 link (li)

100 links = 1 chain (ch) = 4 rods = 66 ft.

80 chains = 1 statute mile = 320 rods = 5,280 ft.

Measurement of the Area by Double Meridian Distance Technique

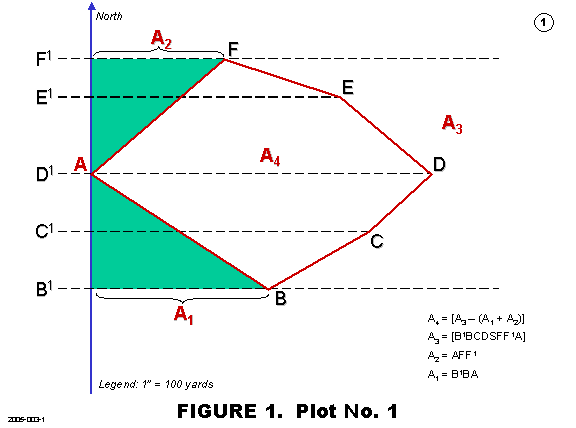
The meridian distance of a traverse line is equal to the length of a line running east to west from the midpoint of the traverse line to a reference meridian. The reference meridian is the meridian that passes through the most westerly traverse station. In Figure #1 (Plot), the dotted lines indicate the meridian distances of the traverse lines to which they extend from the reference meridians.

The following rules for determining meridian distance are outlined below:

1. For the initial traverse line in a closed traverse, the meridian distance equals one half of the departure.

2. For each subsequent traverse line, the meridian distance equals the meridian distance of the preceding course line, plus one half of the departure of the preceding line, plus one half of the departure of the line itself.

If the rules have been followed correctly, the BMD of the last course will be equal to the departure of the last course with its sign changed.

The altitude is the latitude of the course, and the average of the bases of the several courses is equal to the perpendicular distance to each course of the meridian.

Methodology (Equipment Required):

One transit with a Tripod, Stadia Rod, and Data Collection forms shown in Figure #1.

Measurements: The Transit operator will be assisted by one individual to position the Stadia Rod under the command of the Transit Operator. The Transit will measure the range and bearing of the points. It is envisioned that a minimum of ten readings from each side will be taken. Figure #1 illustrates the necessary data elements that must be recorded during the surveying. Columns #1is the station number, Column #2 is the Slant Range, Column #3 Bearing Angle, and Column #4 the elevation angle. Columns #5 thru #10 are the elements of data calculated from the recorded measurements. The analytical results will be calculated before the measurements. The algorithm has been tested and verified -- it works.

Calculations: Table #1 illustrates the series of calculations based on the following measurements: Distance, Bearing, and Altitude. For this project, it is assumed to be in two dimensions excluding the topography and elevation or altitude considerations. The recorded measurements are used to calculate the Latitude, Departure, Double Meridian Distance, and Double Areas. At the end of the calculations, the DMD of the last course should be the same or approximated to the departure of the last course except a different sign.

If they are not the same, a truncation error may have occurred. Figure #1 depicts the geometry of the plot, and Table 1 illustrates the calculations of the plot. A test case has been used to define the area in Distances and Bearing to calculate the Latitude and Longitude of each course line. In essence, the table data elements are the basis to determine the acreage of the land. A table of the liner measure and area measure standards are provided for information only.

The following is a summary of the formulas used to calculate the area of the farm:

St = Slant Distance in yards.

Bo = The azimuth angle to the course line referenced to North.

Latitude = (St)*Sine Bo (Theta)

Departure = (St)* cosine Bo (Theta)

DMD of the first course = Departure of the first course

DMD (1) = (DMD of the first course)+(departure of the preceding point)+(the departure of the current point) Note #1.

Double Areas = (Latitude) * (DMD). Multiply the latitude of the course line by the DMD of the course line. The results will be either positive or negative.

Note#1: The subsequent courses are calculated in the same fashion.

Appendix # 1-Standard Measurement Used In Surveying:

U.S. Weights and Measurements

Linear Measure:

12 inches (in.) = 1 foot (ft.)

3 feet = 1 yard (yd)

51/2 yards = 1 rod (rd), pole, or perch (161/2 ft.)

40 rods = 1 furlong (fur) = 220 yds = 660 ft.

8 furlongs = 1 statute mile (mi.) = 1,760 yds = 5,280 ft.

3 land miles = 1 league

5,280 feet = 1 statute or land mile

6,076.11549 feet = 1 international nautical mile

Area Measure:

144 square inches = 1 sq ft.

9 square feet = 1 sq yd = 1,296 sq in.

301/4 square yards = 1 sq rd = 2721/4 sq ft.

160 square rods = 1 acre = 4,840 sq yds = 43,560 sq ft.

640 acres = 1 sq mi.

1 mile square = 1 section (of land)

6 miles square = 1 township = 36 sections = 36 sq mi.

Gunter's or Surveyor's Chain Measure:

7.92 inches = 1 link (li)

100 links = 1 chain (ch) = 4 rods = 66 ft.

80 chains = 1 statute mile = 320 rods = 5,280 ft.

Table 1: Calculations of Plot #1

Course #	Distance (Yards)	Bearing (Degrees)	SineƟ	COS Ɵ	Latitude	Departure	DM Ɵ	Double +	Areas -
AB	360	122	-.53	.85	-191	306	306		58,446.0
BC	220	63	.45	.89	+162	196	808	130,896
CD	150	45	.71	.71	+106	106	1,110	117,660
DE	250	309	.63	.78	+157	-195	1,021	160,297
EF	200	282	.21	-.98	+ 42	-196	630	26,460
FA	290	225	- .71	-.71	-206	-206	228		47,010
						TOTAL DIFF =		435,313 329,857.00 YARDS	105,456.0

TOTAL DOUBLE AREA (TDA)

TDA = (DIFF) = 329,857.0 = 68.15 ACRES

4840 YDS.(SQ)/ACRE 4840

Cosine Law:

COS A = b² + c² - a²

2bc

COS B = a² + c² - b²

2AC

COS C = a² + b² -c²

2AB

Sine Law:

a = b = c__

Sin A Sin B Sin C

Pythagorean Theorem:

a² = b² + c²

a = √ b² + c² = (A² + b²) ½

Chronology of History of Weights and Measurements

3000 BC: One that gained a certain universal nature was that of the Egyptian cubit developed around 3000 BC. Based on the human body, it was taken to be the length of an arm from the elbow to the extended fingertips.

2500-1700 BC: Harappan civilization flourished in the Punjab between 2500 BC and 1700 BC. The Harappans appear to have adopted a uniform system of weights and measures.

1700 BC: Later civilization whose weights and measures had a wide influence was that of the Babylonians around 1700 BC. Their basic unit of length was, like the Egyptians, the cubit. The Babylonian cubit (530 mm), however, was very slightly longer than the Egyptian cubit (524 mm). The Babylonian cubit was divided into 30 kus, which is interesting since the kus must have been about a finger's breadth, but the fraction ¹/₃₀ is one that is also closely connected to the Babylonian base 60 number system. A Babylonian foot was ²/₃ of a Babylonian cubit.

400 BC: Around 400 BC Athens was a center of trade from a wide area. The Agora was the commercial center of the city and we know from the plays of Aristophanes the type of noisy dealing that went on there.

13^th Century England: England and France measures were developed in rather different ways. We have seen above how the problem of standardization of measures always presented problems, and in early 13^th century England a royal ordinance Assize of Weights and Measures gave a long list of definitions of measurement to be used.

1670: Gabriel Mouton, in 1670, had suggested that the world should adopt a uniform scale of measurement based on the mille, which he defined as the length of one minute of the Earth's arc.

1700: The French, in fact, had more than 1,000 units of measurement by the late 1700s with approximately 250,000 variations in size from one town to another.

1788: In France, on the other hand, there was no standardization and as late as 1788 Arthur Young wrote in "Travels during the years 1787, 1788, 1789" published in 1793: “In France the infinite perplexity of the measures exceeds all comprehension. They differ not only in every province, but in every district and almost every town.”

1789 Lalande, in April 1789, proposed that the measures used in Paris should become national ones, an attempt at standardization but not rationalization.

1790: This proposal was put to the National Assembly in February 1790, but in March a different suggestion was made. Talleyrand put to the National Assembly a proposal due to Condorcet, namely that a new measurement system be adopted based on a length from nature.

The meter (m), which is approximately 39.37 in, was originally defined as one ten-millionth of the distance from the equator to the North Pole on a line running through Paris.

1791: Diplomatic wording allowed an international agreement to be reached, but in March 1791 Borda, as chairman of the Commission of Weights and Measures, proposed using instead of the length of a pendulum, the length of ¹/_10,000,000 of the distance from the pole to the equator of the Earth.

1792-1798: Delambre and Méchain measured the meridian from Dunkerque and Barcelona between 1792 and 1798. Later, after it was discovered that the Earth is not a perfect sphere, the standard meter was defined as the distance between two fine lines marked on a bar of platinum-iridium alloy.

1793: French Revolution progressed to the stage where the Académie des Sciences was abolished in August 1793 but before that Borda, Lagrange and Laplace had computed a provisional value for the meter based on the survey carried out by Cassini de Thury in 1740.

1798: An International Commission began work in September 1798 to replace the provisional values with precise ones computed from the data collected by Delambre and Méchain. By June of the following year the Commission had produced a platinum bar, which became the official definition of the meter.

1799: The meter was required by law to be used in the Paris region. However, as one might expect, introducing the new measure was easier said than done. Part of the problem was that Greek and Latin prefixes like kilo- and centi- had been proposed to help make the new system internationally acceptable but were strongly disliked in France.

1800: An attempt was made to make the system more acceptable by dropping the Greek and Latin prefixes and reinstating the older names for measures but with new metric values.

1801: It became illegal to use any other system of weights and measures anywhere in France, but that was largely ignored.

1812: Napoleon returned the country to its former units.

1820: The decimal metric system was required to be used by law in the Low Countries in 1820.

1821: In 1821 Secretary of State John Quincy Adams, in a report to Congress, advocated the adoption of the metric system.

1830: In 1830 Belgium became independent of Holland and made the metric system, together with its former Greek and Latin prefixes, the only legal measurement system.

1840: In 1840 the French government reintroduced the metric system but it took many years before use of the old measures died out.

1860= In the 1860s Britain, the United States and the German states all made moves towards adopting the metric system.

1864: It became legal in Britain in 1864, but a law that was passed by the House of Commons to require its use throughout the British Empire never made it through its final stages on to the statute books. It is interesting that many leading British scientists were opposed to the introduction of the metric system in Britain in 1864, which is one reason that it only became legal but not compulsory.

1866: In 1866 Congress legalized the use of the metric system, and the system was increasingly adopted, notably in medicine and science, as well as in certain sports such as track and field. The Metric System became legal in the United States.

1868: The German states passed legislation in 1868, which meant that on the unification of these states to form Germany, use of the metric system was made compulsory. George Airy and John Herschel argued strongly against it, as did William Rankine who composed the poem The Three-Foot Rule:

1870: In 1870 an International Conference was convened by the French in Paris. Invitations had been sent to scientists from countries around the world with the aim of improving international scientific cooperation by having the metric system as the world- wide standard. War broke out between France and Prussia just before the delegates were due to arrive, however, and the German delegation did not attend.

1872: Wishing that any decision be a truly international one, the conference was postponed, and it met again in 1872.

1875: The outcome was the setting up of the International Bureau of Weights and Measures, to be situated in Paris, and the Convention of the Meter of 1875 that was signed by seventeen nations. Further countries signed up over the following years.

1889: In 1889 the International Bureau of Weights and Measures replaced the original meter bar in Paris by a new one and at the same time had copies of the bar sent to every country which had signed up to the Convention of the Meter. The definition now became the distance between two lines marked on a standard bar made from 90 percent platinum and 10 percent iridium.

1893: In 1893 the Office of Weights and Measures (now the National Institute of Standards and Technology) of the United States adopted the metric system in legally defining the yard and the pound.

1900: All metric units were originally derived from the meter, but by 1900 the metric system began to be based on the meter-kilogram-second (makes) system.

1901: The unit of volume, the liter, was originally defined as 1 cubic decimeter (dm³), but in 1901 it was redefined as the volume occupied by a kilogram of water at 4°C and 760 mm of mercury.

1956: Indeed the second, then defined as 1/86,400 of the mean solar day, does change but a fixed definition was introduced in 1956 by the International Bureau of Weights and Measures, as ¹/_{31,556,925.9747} of the length of the tropical year 1900.

1960: This remained the standard until 1960 when the International Bureau of Weights and Measures adopted a more accurate standard for international science when it defined the meter in terms of the wavelength of light emitted by the krypton-86 atom, namely 1,650,763.73 wavelengths of the orange-red line in the spectrum of the atom in a vacuum.

1964: It was changed in 1964 to 9,192,631,770 cycles of radiation associated with a particular change of state of the caesium-133 atom. The original definition (dm³) was restored.

1965: In 1965 the United Kingdom became the first of the English-speaking countries to begin an organized effort to abandon the older units of measurement. Canada, Australia, New Zealand, and South Africa quickly followed and adopted the changeover more rapidly than the United Kingdom.

1971: In 1971, after an extensive study, the U.S. secretary of commerce recommended that the United States convert to metric units under a ten-year voluntary plan.

1975: In 1975 President Gerald R. Ford signed the Metric Conversion Act.

1983: The meter was redefined again in 1983, this time as the distance which light travels in a vacuum in ¹/_299,792,458 seconds. This remains the current definition. Note that in all these redefinitions, the value fixed in 1799 by data from the Delambre- Méchain survey always has been used as the baseline.

1983: By 1983 when the meter was defined in terms of the second, Borda's objection was no longer valid as the definition of the second by then did not have the astronomical definition that was indeed variable.

1988: In 1988 a provision in new federal legislation called for all federal agencies to use the metric system in business transactions starting in 1992, but this was never implemented.

BIBLIOGRAPHY

Weights and Measures Article by: J J O'Connor and E F Robertson

MacTutor History of Mathematics, April 2003

[http://www-history.mcs.st-andrews.ac.uk/HistTopics/Measurement.html]