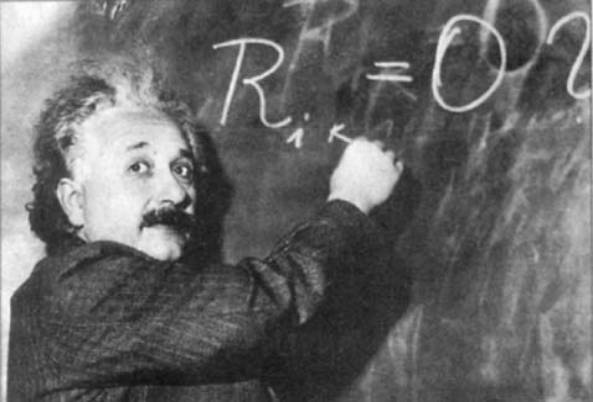Albert Einstein
The Accomplishments of Dr. Albert Einstein
By:
Dr. Francisco J. Collazo
April 6, 2005
April 6, 2005
Dr. Albert Einstein Accomplishments
By: Dr. Francisco J. Collazo
Introduction:
Dr. Albert Einstein was born 14 March 1879 in
Ulm, Wittenberg, Germany and died 18 April 1955 in Princeton, New
Jersey. With his brilliant theoretical
work, German-born American physicist Albert Einstein single-handedly
revolutionized 20th-century physics and opened up many new branches of
scientific research. Throughout his career on all of his work, he
employed the principle of Causality created by Aristotle, in philosophy, a
relationship between a cause and an effect.
In a 1955 article from the Scientific American, Nobel-laureate physicists Niels Bohr of Denmark and Isidor Isaac Rabi of the United States paid tribute to Einstein and discussed the importance of his contributions to physics. Albert Einstein’s elegant equation E=mc2 predicted that energy could be converted to matter. Using a linear accelerator and high-energy laser light, physicists have done just that. After presenting his general theory of relativity in 1915, German-born American physicist Albert Einstein tried in vain to unify his theory of gravitation with one that would include all the fundamental forces in nature.
Around 1886, Albert Einstein began
his school career in Munich. As well as
his violin lessons, which he had from age six to age thirteen, he also had
religious education at home where he was taught Judaism. Two years later he entered the Luitpold
Gymnasium, and after this his religious education was given at school. He studied mathematics, in particular calculus,
beginning around 1891.
In 1894, Einstein's family moved
to Milan but Einstein remained in Munich.
In 1895, Einstein failed an examination that would have allowed him to
study for a diploma as an electrical engineer at the Eidgenössische Technische
Hochschule in Zurich. Einstein
renounced his German citizenship in 1896 and would be stateless for a number of
years. He did not even apply for Swiss citizenship until 1899; his citizenship
was granted in 1901.
Following the failing of the
entrance exam to the ETH, Einstein attended secondary school at Aarau planning
to use this route to enter the ETH in Zurich.
While at Aarau he wrote an essay (for which was only given a little
above half marks!) of his plans for the future.
Albert Einstein once said, “If I
were to have the good fortune to pass my examinations, I would go to
Zurich. I would stay there for four
years in order to study mathematics and physics. I imagined myself becoming a teacher in those branches of the
natural sciences, choosing the theoretical part of them. Here are the reasons that lead me to this
plan. Above all, it is my disposition for abstract and mathematical thought,
and my lack of imagination and practical ability.”
Indeed Einstein succeeded with his
plan graduating in 1900 as a teacher of mathematics and physics. One of his friends at ETH was Marcel
Grossmann who was in the same class as Einstein. Einstein tried to obtain a post; writing to Hurwitz who held out
some hope of a position but nothing came of it. Three of Einstein's fellow students, including Grossmann, were
appointed assistants at ETH in Zurich, but clearly Einstein had not impressed
them enough and in 1901 was still writing universities in the hope of obtaining
a job but without success.
He did manage to avoid Swiss
military service on the grounds that he had flat feet and varicose veins. By mid 1901 he had a temporary job as a
teacher, teaching mathematics at the Technical High School in Winterthur.
Around this time he wrote: - “I have
given up the ambition to get to a university...”
Another temporary position
teaching in a private school in Schaffhausen followed. Then Grossmann's father tried to help
Einstein get a job by recommending him to the director of the patent office in
Bern. Einstein was appointed as a
technical expert third class.
Einstein worked in this patent
office from 1902 to 1909, holding a temporary post when he was first appointed,
but by 1904 the position was made permanent and in 1906 he was promoted to
technical expert second-class. While in
the Bern patent office he completed an astonishing range of theoretical physics
publications, written in his spare time without the benefit of close contact
with scientific literature or colleagues.
Einstein earned a doctorate from the University of Zurich in 1905 for a
thesis on a new determination of molecular dimensions. He dedicated the thesis to Grossmann.
In the first of three papers, all
written in 1905, Einstein examined the phenomenon discovered by Max Planck
according to which electromagnetic energy seemed to be emitted from radiating
objects in discrete quantities. The
energy of these quanta was directly proportional to the frequency of the
radiation. This seemed to contradict
classical electromagnetic theory, based on Maxwell's equations and the laws of
thermodynamics, which assumed that electromagnetic energy consisted of waves,
which could contain any small amount of energy. Einstein used Planck's quantum hypothesis to describe the
electromagnetic radiation of light.
Einstein's second 1905 paper
proposed what is today called the special theory of relativity. He based his new theory on a
reinterpretation of the classical principle of relativity, namely that the laws
of physics had to have the same form in any frame of reference. As a second fundamental hypothesis, Einstein
assumed that the speed of light remained constant in all frames of reference,
as required by Maxwell's theory.
Later in 1905 Einstein showed how
mass and energy were equivalent.
Einstein was not the first to propose all the components of special
theory of relativity. His contribution
is unifying important parts of classical mechanics and Maxwell's
electrodynamics. The third of
Einstein's papers of 1905 concerned statistical mechanics, a field that had
been studied by Ludwig Boltzmann and Josiah Gibbs.
After 1905 Einstein continued
working in the areas described above.
He made important contributions to the quantum theory, but he sought to
extend the special theory of relativity to phenomena involving acceleration. The key appeared in 1907 with the principle
of equivalence, in which gravitational acceleration was held to be
indistinguishable from acceleration caused by mechanical forces. Gravitational mass was therefore identical
with inertial mass.
In 1908 Einstein became a lecturer
at the University of Bern after submitting his Habilitation Thesis Consequences
for the constitution of radiation following from the energy distribution law of
black bodies. The following year he
became a professor of physics at the University of Zurich, having resigned his
lectureship at Bern and his job in the patent office in Bern.
By 1909 Einstein was recognized as
a leading scientific thinker and in that year he resigned from the patent
office. He was appointed to a full
professor at the Karl-Ferdinand University in Prague in 1911. In fact 1911 was a very significant year for
Einstein since he was able to make preliminary predictions about how a ray of
light from a distant star, passing near the Sun, would appear to be bent
slightly in the direction of the Sun.
This would be highly significant, as it would lead to the first
experimental evidence in favor of Einstein's theory.
About 1912, Einstein began a new
phase of his gravitational research, with the help of his mathematician friend
Marcel Grossmann, by expressing his work in terms of the tensor calculus of
Tullio Levi-Civita and Gregorio Ricci-Curbastro. Einstein called his new work the general theory of
relativity. He moved from Prague to
Zurich in 1912 to take up a chair at the Eidgenössische Technische Hochschule
in Zurich.
Einstein returned to Germany in
1914 but did not reapply for German citizenship. What he accepted was an impressive offer. It was a research position in the Prussian
Academy of Sciences together with a chair (but no teaching duties) at the
University of Berlin. He was also
offered the directorship of the Kaiser Wilhelm Institute of Physics in Berlin,
which was about to be established.
Late in 1915, after a number of
false starts, Einstein published the definitive version of general theory of
relativity. Just before publishing this
work he lectured on general relativity at Göttingen and he wrote: - “To my great joy, I completely succeeded in
convincing Hilbert and Klein.”
In fact Hilbert submitted for
publication, a week before Einstein completed his work, a paper that contains
the correct field equations of general relativity.
When British eclipse expeditions
in 1919 confirmed his predictions, the popular press idolized Einstein. The London Times ran the headline on 7
November 1919: - “Revolution in science - New theory of the Universe -
Newtonian ideas overthrown.”
In 1920 Einstein's lectures in
Berlin were disrupted by demonstrations, which, although officially denied,
were almost certainly anti-Jewish.
Certainly there were strong feelings expressed against his works during
this period which Einstein replied to in the press quoting Lorentz, Planck and
Eddington as supporting his theories and stating that certain Germans would
have attacked them if he had been: -
“…A German national with or without swastika instead of a Jew with
liberal international convictions...”
During 1921 Einstein made his
first visit to the United States. His
main reason was to raise funds for the planned Hebrew University of
Jerusalem. However he received the Barnard
Medal during his visit and lectured several times on relativity. He is reported to have commented to the
chairman at the lecture he gave in a large hall at Princeton, which was
overflowing with people: - “I never realized that so many Americans were
interested in tensor analysis.”
Einstein received the Nobel Prize
in 1921 but not for relativity rather for his 1905 work on the photoelectric
effect. In fact he was not present in
December 1922 to receive the prize, being on a voyage to Japan. Around this time he made many international
visits. He had visited Paris earlier in 1922 and during 1923 he visited
Palestine. After making his last major
scientific discovery on the association of waves with matter in 1924 he made
further visits in 1925, this time to South America.
Among further honors, which
Einstein received, were the Copley Medal of the Royal Society in 1925 and the
Gold Medal of the Royal Astronomical Society in 1926.
Niels Bohr and Einstein were to
carry on a debate on quantum theory, which began at the Solvay Conference in
1927. Planck, Niels Bohr, de Broglie,
Heisenberg, Schrödinger and Dirac were at this conference, in addition to
Einstein. Einstein had declined to give
a paper at the conference and: - “ ...
Said hardly anything beyond presenting a very simple objection to the
probability interpretation.... Then he fell back into silence...”
Indeed Einstein's life had been
hectic and he was to pay the price in 1928 with a physical collapse brought on
through overwork. However he made a
full recovery despite having to take things easy throughout 1928.
By 1930 he was making
international visits again, back to the United States. A third visit to the United States in 1932
was followed by the offer of a post at Princeton. The idea was that Einstein would spend seven months a year in
Berlin and five months at Princeton.
Einstein accepted and left Germany in December 1932 for the United
States. The following month the Nazis came to power in Germany and Einstein was
never to return there.
During 1933 Einstein traveled in
Europe visiting Oxford, Glasgow, Brussels and Zurich. Offers of academic posts,
which he had found it so hard to get in 1901, were plentiful. He received offers from Jerusalem, Leaden,
Oxford, Madrid and Paris.
What was intended only as a visit
became a permanent arrangement by 1935 when he applied and was granted
permanent residency in the United States.
At Princeton his work attempted to unify the laws of physics. However he was attempting problems of great
depth and he wrote: - “I have locked
myself into quite hopeless scientific problems - the more so since, as an
elderly man, I have remained estranged from the society here...”
In 1940 Einstein became a citizen
of the United States, but chose to retain his Swiss citizenship. He made many contributions to peace during
his lifetime. In 1944 he made a
contribution to the war effort by hand writing his 1905 paper on special
relativity and putting it up for auction.
It raised six million dollars, the manuscript today being in the Library
of Congress.
By 1949 Einstein was not
well. A spell in a hospital helped him
recover but he began to prepare for death by drawing up his will in 1950. He left his scientific papers to the Hebrew
University in Jerusalem, a university that he had raised funds for on his first
visit to the USA. He served as a
governor of the university from 1925 to 1928, but he had turned down the offer
of a post in 1933, as he was very critical of its administration.
One more major event was to take
place in his life. After the death of the first president of Israel in 1952,
the Israeli government decided to offer the post of second president to
Einstein. He refused but found the
offer an embarrassment since it was hard for him to refuse without causing
offence.
One week before his death Einstein
signed his last letter. It was a letter
to Bertrand Russell in which he agreed that his name should go on a manifesto
urging all nations to give up nuclear weapons.
It is fitting that one of his last acts was to argue, as he had done all
his life, for international peace.
Einstein was cremated at Trenton,
New Jersey at 4 pm on 18 April 1955 (the day of his death). His ashes were scattered at an undisclosed
place.
Albert Einstein’s Unknown Personal Traits
Religious Upbringing: Einstein excluded most of what he called
"the merely personal." He
wrote that when still very young, he had searched for an escape from the
seemingly hopeless and demoralizing chase after one's desires and
strivings. That escape offered itself
first in religion. Although brought up
as the son of "entirely irreligious (Jewish) parents," through the
teaching in his Catholic primary school, mixed with his private instruction in
elements of the Jewish religion, Einstein found within himself a "deep
religiosity"– indeed, "the religious paradise of youth."
Einstein’s Sister Maja: Maja made a plausible extrapolation:
that Einstein's "religious feeling" found expression in later years
in his deep interest and actions to ameliorate the difficulties to which fellow
Jews were being subjected, actions ranging from his fights against
anti-Semitism to his embrace of Zionism (in the hope, as he put it in one of
his speeches [April 20, 1935], that it would include a "peaceable and
friendly cooperation with the Arab people"). As we shall see, Maja's extrapolation of the reach of her
brother's early religious feelings might well have gone much further.
Einstein’s Beliefs on Life: In Einstein’s view of a world picture,
the scientist could place the "center of gravity of his emotional life [Gefühlsleben]." And in a sentence with special significance,
he added that persevering in the most difficult scientific problems requires
"a state of feeling [Gefühlszustand] similar to that of a religious
person or a lover."
Evolution
of Religion: In the
evolution of religion, he remarked, there were three developmental stages. At
the first, "with primitive man it is above all fear that evokes religious
notions. This 'religion of fear' . . . is in an important degree stabilized by
the formation of a special priestly caste" that colludes with secular
authority to take advantage of it for its own interest. The next step –
"admirably illustrated in the Jewish scriptures" – was a moral
religion embodying the ethical imperative, "a development [that] continued
in the New Testament." Yet it had a fatal flaw: "the anthropomorphic
character of the concept of God," easy to grasp by "underdeveloped
minds" of the masses while freeing them of responsibility.
This flaw disappears at
Einstein's third, mature stage of religion, to which he believed mankind is now
reaching and which the great spirits (he names Democritus, St. Francis of
Assisi, and Spinoza) had already attained – namely, the "cosmic religious
feeling" that sheds all anthropomorphic elements. In describing the driving motivation toward
that final, highest stage, Einstein uses the same ideas, even some of the same
phrases, with which he had celebrated first his religious and then his
scientific paradise: "The individual feels the futility of human desires,
and aims at the sublimity and marvelous order which reveal themselves both in
nature and in the world of thought.
Individual existence impresses
him as a sort of prison, and he wants to experience the universe as a
single, significant whole." Of
course! Here as always, there has to be the intoxicating experience of
unification. And so Einstein goes on,
"I maintain that the cosmic religious feeling is the strongest and noblest
motive for scientific research . . . . A contemporary has said not unjustly
that in this materialistic age of ours the serious scientific workers are the
only profoundly religious people."
Integration of Religion and
Science - "The Integration of Religion and
Science," Merton notes that among the scientists he studied, "the
religious ethic, considered as a social force, so consecrated science as to
make it a highly respected and laudable focus of attention." The social scientist Bernard H. Gustin
elaborated on this perception, writing that science at the highest level is
charismatic because scientists devoted to such tasks are "thought to come
into contact with what is essential in the universe." I believe this is precisely why so many who
knew little about Einstein's scientific writing flocked to catch a glimpse of
him and to this day feel somehow uplifted by contemplating his iconic image.
Job Failure: Einstein could not find a job in physics upon graduating from college, and became a technical assistant in the Swiss Patent Office. He worked on theoretical physics in his spare time.
Nobel Prize: Einstein did not receive a Nobel Prize for his theory of relativity.
Hitler’s Rise: Einstein immediately left Germany for the United States following Hitler's rise to power.
Field Theory: Einstein spent much of his later career searching for a unified field theory, but was unsuccessful.
Presidency: Einstein declined the presidency of the state of Israel when state leaders offered it to him in 1952.
Einsteinium: The element einsteinium, discovered in 1952, was named in honor of Albert Einstein. Einstein, Albert (1879-1955), German-born American physicist and Nobel laureate, best known as the creator of the special and general theories of relativity and for his bold hypothesis concerning the particle nature of light. He is perhaps the most well known scientist of the 20th century.
Speech Delay: Einstein was born in Ulm on March 14, 1879, and spent his youth in Munich, where his family owned a small shop that manufactured electric machinery. He did not talk until the age of three, but even as a youth he showed a brilliant curiosity about nature and an ability to understand difficult mathematical concepts. At the age of 12 he taught himself Euclidean geometry.
Einstein, a Maverick in his Early Years: Einstein hated the dull regimentation and unimaginative spirit of school in Munich. When repeated business failure led the family to leave Germany for Milan, Italy, Einstein, who was then 15 years old, used the opportunity to withdraw from the school. He spent a year with his parents in Milan, and when it became clear that he would have to make his own way in the world, he finished secondary school in Aarau, Switzerland, and entered the Swiss Federal Institute of Technology in Zurich. Einstein did not enjoy the methods of instruction there. He often cut classes and used the time to study physics on his own or to play his beloved violin. He passed his examinations and graduated in 1900 by studying the notes of a classmate. His professors did not think highly of him and would not recommend him for a university position.
Working in the Patent Office: For two years Einstein worked as a tutor and substitute teacher. In 1902 he secured a position as an examiner in the Swiss patent office in Bern. Einstein remained at the patent office for four years after his star began to rise within the physics community.
Marriage: In 1903 he married Mileva Maric, who had been his classmate at the polytechnic. They had two sons but eventually divorced. Einstein later remarried.
Advanced Education: In 1905 Einstein received his doctorate from the University of Zurich for a theoretical dissertation on the dimensions of molecules, and he also published three theoretical papers of central importance to the development of 20th-century physics.
Educator: Einstein did have important supporters, however. His chief early patron was the German physicist Max Planck. He then moved rapidly upward in the German-speaking academic world. His first academic appointment was in 1909 at the University of Zurich. In 1911 he moved to the German-speaking University at Prague, and in 1912 he returned to the Swiss National Polytechnic in Zurich. Finally, in 1914, he was appointed director of the Kaiser Wilhelm Institute for Physics in Berlin.
Zionism: The two social movements that received his full support were pacifism and Zionism. During World War I he was one of a handful of German academics willing to publicly decry Germany’s involvement in the war. After the war his continued public support of pacifist and Zionist goals made him the target of vicious attacks by anti-Semitic and right wing elements in Germany. Even his scientific theories were publicly ridiculed, especially the theory of relativity.
Germany Exit Hitler in Power: When Hitler came to power, Einstein immediately decided to leave Germany for the United States. He took a position at the Institute for Advanced Study at Princeton, New Jersey. While continuing his efforts on behalf of world Zionism, Einstein renounced his former pacifist stand in the face of the awesome threat to humankind posed by the Nazi regime in Germany.
Disarmament Conference: Albert Einstein became an avowed pacifist during World War I (1914-1918) and continued to speak out for antiwar efforts throughout his life, although he renounced pacifism in the 1930s in the face of the threat to humanity posed by Nazi Germany. In this message, written from Berlin, Germany, in 1931, Einstein stresses the importance of the upcoming World Disarmament Conference, held in 1932. The conference did not produce any substantive agreements, however, and Einstein left Germany in 1933 when Nazi leader Adolf Hitler came to power.
Einstein’s
Biggest Blunder: Two years later, when he expanded his
general relativity to include "cosmological considerations," Einstein
found to his dismay that his system of equations did "not allow the
hypothesis of a spatially closed-ness of the world [raeumliche
Geschlossenheit]." How did
Einstein cure this flaw? By something he
had done very rarely: making an ad hoc addition, purely for convenience:
"We can add on the left side of the field equation a – for the time being
– unknown universal constant, - ![]() ['lambda']." In fact, it seems that not much harm is done
thereby. It does not change the
covariance; it still corresponds with the observation of motions in the solar system
("as long as
['lambda']." In fact, it seems that not much harm is done
thereby. It does not change the
covariance; it still corresponds with the observation of motions in the solar system
("as long as ![]() is
small"), and so forth.
is
small"), and so forth.
Moreover, the proposed new
universal constant ![]() also
determines the average density of the universe with which it can remain in
equilibrium, and provides the radius and volume of a presumed spherical
universe. Altogether a beautiful,
immutable universe – one an immutable God could be identified with. But in 1922, Alexander Friedmann showed that
the equations of general relativity did allow expansion or contraction. And in 1929 Edwin Hubble found by
astronomical observations the fact that the universe does expand. Thus Einstein
– at least according to the physicist George Gamow – remarked that
"inserting
also
determines the average density of the universe with which it can remain in
equilibrium, and provides the radius and volume of a presumed spherical
universe. Altogether a beautiful,
immutable universe – one an immutable God could be identified with. But in 1922, Alexander Friedmann showed that
the equations of general relativity did allow expansion or contraction. And in 1929 Edwin Hubble found by
astronomical observations the fact that the universe does expand. Thus Einstein
– at least according to the physicist George Gamow – remarked that
"inserting ![]() was
the biggest blunder of my life."
was
the biggest blunder of my life."
Albert Einstein and Sigmud Freud Correspond
about the Consequences of War:
In 1932 Albert Einstein and Sigmund Freud
corresponded on the subject of war.
This is a summary of Einstein's letter to Freud.
The Society of Art and Letters wanted to encourage thinkers from
different fields to correspond with each other on topics in the hope the League
of Nations may benefit from it.
Einstein was one of the first to come forward and was given free choice
of topic and partner. He chose Freud,
who agreed to participate. The
correspondence took place in 1932 and was first published in 1933 in Paris
simultaneously in French, German and English (the original correspondence was
in German). Einstein had done some
thinking on the nature of war and why it persisted throughout human history,
despite its devastating effects. He
wrote to Freud stating his own thoughts and asking for Freud's opinion as a
psychologist. Freud replied, agreeing
with most of Einstein's conclusions and adding his own thoughts on each of the
issues by addressing each separately, and posing a question of his own. The following is a summary of Einstein's
Letter dated 30 July 1932:
Einstein expresses how happy he is through the initiative
of the League of Nations to correspond with a person of his choice, and that
the opportunity offers a unique chance to discuss what he considers the most
important question currently facing civilization with Freud. He then goes straight to the question:
"Is there a way to free people from the spectre of war?"
He says: "It has become apparent that through the
advances of technology it is now possible to wipe out humankind. Despite this fact all attempts at a solution
have failed frighteningly. People who
are involved in avoiding war in practice, through their professions (e.g.
diplomats, politicians, peace organizations) have reached a point, partly out
of a feeling of helplessness, where they would welcome the input of people who
have gained a certain amount of distance to all life questions due to their
scientific work."
Einstein says his thinking gives him little insight into the depths of human feelings and desires. Therefore, all he can do is to pose the questions and give answers he hopes Freud can expand on, due to his "deep insight into human urges and desires." Further, Einstein hopes Freud will be able to point to apolitical ways of education that could remove psychological barriers that a normal person does not see.
Scientific Accomplishments and Publications
Threat of the Atomic Bomb: Einstein was one of several concerned physicists who collaborated on this in a letter to President Roosevelt informing him of the possibility of an unimaginably powerful and dangerous new weapon, the atomic bomb. In the first dark days of World War II, these physicists believed that the Germans were already at work on an atomic bomb, using the results of French and American research. Einstein's letter undoubtedly helped to convince President Roosevelt that the United States had to develop its own atomic weapons program quickly.
After World War II, he became a strong advocate for
disarmament, but he was also an outspoken political activist. In this excerpt, he discusses the dangers
faced by the world following the invention of the atomic bomb. Einstein discussed his special and general theories of
relativity and his work toward a unified field theory in a 1950 Scientific
American article. At the time, he was
not convinced that he had discovered a valid solution capable of extending his
general theory of relativity to other forces. Albert Einstein died in 1955, leaving this
problem unsolved.
Einstein’s Letter to FDR: Einstein was one of several concerned physicists who collaborated on this letter to President Roosevelt, informing him of the possibility of an unimaginably powerful and dangerous new weapon: the atomic bomb. In the first dark days of World War II, these physicists believed that the Germans were already at work on an atomic bomb, using the results of French and American research. Einstein's letter undoubtedly helped to convince President Roosevelt that the United States had to develop its own atomic weapons program quickly.
Albert Einstein
Old Grove Rd. Nassau Point
Peconic, Long Island
August 2nd, 1939
F.D. Roosevelt,
President of the United States
White House
Washington, D.C.
Sir: Some recent work by E. Fermi and L. Szilard, which has been communicated to me in manuscript, leads me to expect that the element uranium may be turned into a new and important source of energy in the immediate future. Certain aspects of the situation which has arisen seem to call for watchfulness and, if necessary, quick action on the part of the Administration. I believe therefore that it is my duty to bring to your attention the following facts and recommendations: In the course of the last four months it has been made probable—through the work of Joliot in France as well as Fermi and Szilard in America—that it may become possible to set up a nuclear chain reaction in a large mass of uranium, by which vast amounts of power and large quantities of new radium-like elements would be generated. Now it appears almost certain that this could be achieved in the immediate future.
This new phenomenon would also lead to the construction of bombs, and it is conceivable—though much less certain—that extremely powerful bombs of a new type may thus be constructed. A single bomb of this type, carried by boat and exploded in a port, might very well destroy the whole port together with some of the surrounding territory. However, such bombs might very well prove to be too heavy for transportation by air.
The United States has only very poor ores of uranium in moderate quantities. There is some good ore in Canada and the former Czechoslovakia, while the most important source of uranium is Belgian Congo.
In view of this situation you may think it desirable to have some permanent contact maintained between the Administration and the group of physicists working on chain reactions in America. One possible way of achieving this might be for you to entrust with this task a person who has your confidence and who could perhaps serve in an unofficial capacity. His task might comprise the following:
a) Approach Government Departments, keep them informed of the further development, and put forward recommendations for Government action, giving particular attention to the problem of securing a supply of uranium ore for the United States;
b) Speed up the experimental work, which is at present being carried on within the limits of the budgets of University laboratories, by providing funds, if such funds be required, through his contacts with private persons who are willing to make contributions for this cause, and perhaps also by obtaining the co-operation of industrial laboratories which have the necessary equipment.
I understand that Germany has actually stopped the sale of uranium from the Czechoslovakian mines, which she has taken over. That she should have taken such early action might perhaps be understood on the ground that the son of the German Under-Secretary of State, von Weizsäcker, is attached to the Kaiser-Wilhelm-Institute in Berlin where some of the American work on uranium is now being repeated. Yours very truly.
Albert Einstein was
most famous for his contributions to theoretical physics, but he was also
active in social and political causes such as Zionism and political
freedom.
In the first of three seminal papers that were published in 1905, Einstein examined the phenomenon discovered by Max Planck, according to which electromagnetic energy seemed to be emitted from radiating objects in quantities that were ultimately discrete. The energy of these emitted quantities, the so-called light-quanta, was directly proportional to the frequency of the radiation. This circumstance was perplexing because classical electromagnetic theory, based on Maxwell's equations and the laws of thermodynamics, had assumed that electromagnetic energy consisted of waves propagating in a hypothetical, all-pervasive medium called the aluminiferous ether, and that the waves could contain any amount of energy no matter how small.
Einstein used Planck's quantum hypothesis to describe visible electromagnetic radiation, or light. According to Einstein's heuristic viewpoint, light could be imagined to consist of discrete bundles of radiation. Einstein used this interpretation to explain the photoelectric effect, by which certain metals emit electrons when illuminated by light with a given frequency. Einstein's theory, and his subsequent elaboration of it, formed the basis for much of quantum mechanics.
The second of Einstein's 1905
papers proposed what is today called the special theory of relativity. At the time Einstein knew that, according to
Hendrik Antoon Lorentz's theory of electrons, the mass of an electron increased
as the velocity of the electron approached the velocity of light. Einstein also knew that the electron theory,
based on Maxwell's equations, carried along with it the assumption of
aluminiferous ether, but that attempts to detect the physical properties of the
ether had not succeeded. Einstein
realized that the equations describing the motion of an electron in fact could
describe the non-accelerated motion of any particle or any suitably defined
rigid body. He based his new kinematics
on a reinterpretation of the classical principle of relativity that the laws of
physics had to have the same form in any frame of reference.
As a second fundamental
hypothesis, Einstein assumed that the speed of light remained constant in all
frames of reference, as required by classical Maxwellian theory. Einstein abandoned the hypothesis of the
ether, for it played no role in his kinematics or in his reinterpretation of
Lorentz's theory of electrons. As a
consequence of his theory Einstein recovered the phenomenon of time dilatation,
wherein time, analogous to length and mass, is a function of the velocity of a
frame of reference. Later in 1905,
Einstein elaborated how, in a certain manner of speaking, mass and energy were
equivalent. Einstein was not the first to propose all the elements that went into
the special theory of relativity; his contribution lies in having unified
important parts of classical mechanics and Maxwellian electrodynamics.
The third of Einstein's seminal
papers of 1905 concerned statistical mechanics, a field of study that had been
elaborated by, among others, Ludwig Boltzmann and Josiah Willard Gibbs. Unaware of Gibbs' contributions, Einstein
extended Boltzmann's work and calculated the average trajectory of a
microscopic particle buffeted by random collisions with molecules in a fluid or
in a gas. Einstein observed that his
calculations could account for Brownian motion, the apparently erratic movement
of pollen in fluids, which had been noted by the British botanist Robert
Brown. Einstein's paper provided
convincing evidence for the physical existence of atom-sized molecules, which
had already received much theoretical discussion. His results were independently discovered by the Polish physicist
Marian von Smoluchowski and later elaborated by the French physicist Jean
Perrin.
Mass Energy Equation: Even more important is the relation between the mass m and energy E. They are coupled by the relation E = mc2, and because c is very large, the energy equivalence of a given mass is enormous. The change of mass giving an energy change is significant in nuclear reactions, as in reactors or nuclear weapons, and in the stars, where a significant loss of mass accompanies the huge energy release.
Fission of Weapons: In 1905 Albert Einstein published his special theory of relativity. According to this theory, the relation between mass and energy is expressed by the equation E = mc2, which states that a given mass (m) is associated with an amount of energy (E) equal to this mass multiplied by the square of the speed of light (c). A very small amount of matter is equivalent to a vast amount of energy. For example, 1 kg (2.2 lb) of matter converted completely into energy would be equivalent to the energy released by exploding 22 megatons of TNT.
Fundamental Ideas and Methods
of Relativity: It
contains the passage in which Einstein revealed what in his words was "the
happiest thought of my life" [der gluecklichste Gedanke meines Lebens]
– a thought experiment that came to him in 1907: nothing less than the
definition of the equivalence principle, later developed in his general relativity
theory. It occurred to Einstein –
thinking first of all in visual terms, as was usual for him – that if a man
were falling from the roof of his house and tried to let anything drop, it
would only move alongside him, thus indicating the equivalence of acceleration
and gravity. In Einstein's words,
"the acceleration of free fall with respect to the material is therefore a
mighty argument that the postulate of relativity is to be extended to
coordinate systems that move non-uniformly relative to one another . . .
."
Faraday
Experiment: For the
present purpose I want to draw attention to another passage in that
manuscript. His essay actually begins
in a largely impersonal, pedagogic tone, similar to that of his first popular
book on relativity, published in 1917.
But in a surprising way, in the section titled "General Relativity
Theory," Einstein suddenly
switches to a personal account. He
reports that in the construction of the special theory, the "thought
concerning the Faraday [experiment] on electromagnetic induction played for me
a leading role." He then describes
that old experiment, in words similar to the first paragraph of his 1905
relativity paper, concentrating on the well-known fact, discovered by Faraday
in 1831, that the induced current is the same whether it is the coil or the
magnet that is in motion relative to the other, whereas the "theoretical
interpretation of the phenomenon in these two cases is quite
different."
While other physicists, for many
decades, had been quite satisfied with that difference, here Einstein reveals a
central preoccupation at the depth of his soul: "The thought that one is
dealing here with two fundamentally different cases was for me unbearable [war
mir unertraeglich]. The difference
between these two cases could not be a real difference . . . . The phenomenon
of the electromagnetic induction forced me to postulate the (special) relativity
principle."
Cardinal O’Connell’s Views on
the Relativity Theory: In
1929, Boston's Cardinal O'Connell branded Einstein's theory of relativity as
"befogged speculation producing universal doubt about God and His
Creation," and as implying "the ghastly apparition of atheism."
In alarm, New York's Rabbi Herbert S. Goldstein asked Einstein by telegram: "Do
you believe in God? Stop. Answer paid 50 words." In his response, for which Einstein needed but twenty-five
(German) words, he stated his beliefs succinctly: "I believe in Spinoza's
God, Who reveals Himself in the lawful harmony of the world, not in a God Who
concerns Himself with the fate and the doings of mankind." The rabbi cited this as evidence that
Einstein was not an atheist, and further declared that "Einstein's theory,
if carried to its logical conclusion, would bring to mankind a scientific
formula for monotheism." Einstein wisely remained silent on that point.
The World as I See It: "How strange is the lot of us
mortals! Each of us is here for a brief
sojourn; for what purpose he knows not, though he sometimes thinks he senses
it. But without deeper reflection one knows from daily life that one exists for
other people -- first of all for those upon whose smiles and well being our own
happiness is wholly dependent, and then for the many, unknown to us, to whose
destinies we are bound by the ties of sympathy. A hundred times every day I remind myself that my inner and outer
life are based on the labors of other men, living and dead, and that I must
exert myself in order to give in the same measure as I have received and am
still receiving...
"I have never looked upon
ease and happiness as ends in themselves -- this critical basis I call the
ideal of a pigsty. The ideals that have
lighted my way, and time after time have given me new courage to face life
cheerfully, have been Kindness, Beauty, and Truth. Without the sense of kinship
with men of like mind, without the occupation with the objective world, the
eternally unattainable in the field of art and scientific endeavors, life would
have seemed empty to me. The trite objects
of human efforts -- possessions, outward success, and luxury -- have always
seemed to me contemptible.
"My passionate sense of
social justice and social responsibility has always contrasted oddly with my
pronounced lack of need for direct contact with other human beings and human
communities. I am truly a 'lone
traveler' and have never belonged to my country, my home, my friends, or
even my immediate family, with my whole heart; in the face of all these
ties, I have never lost a sense of distance and a need for solitude..."
"My political ideal is democracy. Let every man be respected as an individual and no man idolized. It is an irony of fate that I myself have been the recipient of excessive admiration and reverence from my fellow-beings, through no fault, and no merit, of my own. The cause of this may well be the desire, unattainable for many, to understand the few ideas to which I have with my feeble powers attained through ceaseless struggle. I am quite aware that for any organization to reach its goals, one man must do the thinking and directing and generally bear the responsibility. But the led must not be coerced, they must be able to choose their leader. In my opinion, an autocratic system of coercion soon degenerates; force attracts men of low morality... The really valuable thing in the pageant of human life seems to me not the political state, but the creative, sentient individual, the personality; it alone creates the noble and the sublime, while the herd as such remains dull in thought and dull in feeling.
"This topic brings me to
that worst outcrop of herd life, the military system, which I abhor... This
plague-spot of civilization ought to be abolished with all possible speed.
Heroism on command, senseless violence, and all the loathsome nonsense that
goes by the name of patriotism -- how passionately I hate them!
"The most beautiful
experience we can have is the mysterious.
It is the fundamental emotion that stands at the cradle of true art and
true science. Whoever does not know it
and can no longer wonder, no longer marvel, is as good as dead, and his eyes
are dimmed. It was the experience of
mystery -- even if mixed with fear -- that engendered religion. A knowledge of the existence of something we
cannot penetrate, our perceptions of the profoundest reason and the most
radiant beauty, which only in their most primitive forms are accessible to our
minds: it is this knowledge and this emotion that constitute true
religiosity. In this sense, and only
this sense, I am a deeply religious man...
I am satisfied with the mystery of life's eternity and with a knowledge,
a sense, of the marvelous structure of existence -- as well as the humble
attempt to understand even a tiny portion of the Reason that manifests itself
in nature."
![]()
Theory of Relativity: Einstein’s third major paper in 1905, “On the Electrodynamics of Moving Bodies,” contained what became known as the special theory of relativity. Since the time of the English mathematician and physicist Sir Isaac Newton, natural philosophers (as physicists and chemists were known) had been trying to understand the nature of matter and radiation, and how they interacted in some unified world picture. The position that mechanical laws are fundamental has become known as the mechanical worldview, and the position that electrical laws are fundamental has become known as the electromagnetic worldview. Neither approach, however, is capable of providing a consistent explanation for the way radiation (light, for example) and matter interact when viewed from different inertial frames of reference, that is, an interaction viewed simultaneously by an observer at rest and an observer moving at uniform speed.
In the spring of 1905, after considering these problems for ten years, Einstein realized that the crux of the problem lay not in a theory of matter but in a theory of measurement. At the heart of his special theory of relativity was the realization that all measurements of time and space depend on judgments as to whether two distant events occur simultaneously. This led him to develop a theory based on two postulates: the principle of relativity, that physical laws are the same in all inertial reference systems, and the principle of the invariance of the speed of light, that the speed of light in a vacuum is a universal constant. He was thus able to provide a consistent and correct description of physical events in different inertial frames of reference without making special assumptions about the nature of matter or radiation, or how they interact. Virtually no one understood Einstein’s argument.
Einstein Approach: Einstein in all his work employed the principle Causality created by Aristotle, in philosophy, the relationship of a cause to its effect. The difficulty that others had with Einstein’s work was not because it was too mathematically complex or technically obscure; the problem resulted, rather, from Einstein’s beliefs about the nature of good theories and the relationship between experiment and theory. Although he maintained that the only source of knowledge is experience, he also believed that scientific theories are the free creations of a finely tuned physical intuition and that the premises on which theories are based cannot be connected logically to experiment. A good theory, therefore, is one in which a minimum number of postulates is required to account for the physical evidence. This sparseness of postulates, a feature of all Einstein’s work, was what made his work so difficult for colleagues to comprehend, let alone support.
The Ritz-Einstein Agreement to Disagree: During 1908 and 1909 Ritz and Einstein
battled over what we now call the time arrows of electrodynamics and
entropy. Ritz argued that
electrodynamic irreversibility was one of the roots of the second law of
thermodynamics, while Einstein defended Maxwell-Lorentz electromagnetic time
symmetry. Microscopic reversibility
remains a cornerstone of our current paradigm, yet we are finding more and more
evidence that experimentally discerned time arrows are asymmetrical and that
they all point from past to future.
This paper furnishes some comments about events leading up to the
Ritz-Einstein confrontation, some subsequent developments, and an English
translation of their agreement to disagree.
A side-by-side comparison of two recent summaries of their battle
communiques is included to provide an overview of what they had to say about
this current issue.
Einstein’s
Contribution to the Big Bang Theory: The theory is based on
the mathematical equations, known as the field equations, of the general
theory of relativity set forth in 1915 by Albert Einstein. The overall framework of the big
bang theory came out of solutions to Einstein’s general relativity field equations
and remains unchanged, but various details of the theory are still being
modified today. Einstein himself initially believed that the universe was static. When his equations seemed to imply that the universe was expanding or contracting,
Einstein added a constant term to cancel out the expansion or contraction of
the universe. When the expansion of the universe
was later discovered, Einstein stated that introducing this “cosmological
constant” had been a mistake.
After Einstein’s work of 1917, several scientists, including
the abbé Georges Lemaître in Belgium, Willem de Sitter in Holland, and
Alexander Friedmann in Russia, succeeded in finding solutions to Einstein’s
field equations. The universes described by the different
solutions varied. De Sitter’s model had
no matter in it. This model is actually
not a bad approximation since the average density of the universe is extremely low. Lemaître’s universe
expanded from a “primeval atom.” Friedmann’s universe
also expanded from a very dense clump of matter, but did not involve the
cosmological constant. These models
explained how the universe behaved
shortly after its creation, but there was still no satisfactory explanation for
the beginning of the universe.
Black Hole Application of the Relativity Theory: Black holes are objects that are so massive and dense that their immense gravitational pull does not even let light escape. If the core left over after a supernova explosion has a mass of more than about fives times that of the Sun, the force holding up the neutrons in the core is not large enough to balance the inward gravitational force. No outward force is large enough to resist the gravitational force. The core of the star continues to collapse.
When the core's mass is sufficiently concentrated, the gravitational force of the core is so strong that nothing, not even light, can escape it. The gravitational force is so strong that classical physics no longer applies, and astronomers use Einstein’s general theory of relativity to explain the behavior of light and matter under such strong gravitational forces. According to general relativity, space around the core becomes so warped that nothing can escape, creating a black hole. A star with a mass ten times the mass of the Sun would become a black hole if it were compressed to 90 km (60 mi) or less in diameter.
Einsteinium: Einsteinium, symbol Es, artificially created radioactive element with an atomic number of 99. Einsteinium is one of the transuranium elements in the actinide series of the periodic table (see Periodic Law). Isotopes of einsteinium with mass numbers ranging from 243 to 256 are known. The element, named in honor of German-born American physicist Albert Einstein, was discovered in 1952 in the debris produced by a thermonuclear explosion (see Nuclear Weapons). The isotope first identified had an atomic mass of 253 and a half-life of 20 days. Subsequently, the most long-lived of all the known einsteinium isotopes, einsteinium-252, was prepared by irradiating plutonium in a nuclear reactor; however, only small amounts are now being produced
1919 Sun Eclipse Main Event: Since the only forces at work between the galaxies that make up the material universe are the forces of gravity, the cosmological problem is closely connected with the theory of gravitation, in particular with its modern version as comprised in Albert Einstein's general theory of relativity. In the frame of this theory the properties of space, time and gravitation are merged into one harmonious and elegant picture. On the basis of the general theory of relativity, Einstein accounted for the previously unexplained variations in the orbital motion of the planets and predicted the bending of starlight in the vicinity of a massive body such as the sun. The confirmation of this latter phenomenon during an eclipse of the sun in 1919 became a media event, and Einstein’s fame spread worldwide.
For the rest of his life Einstein devoted considerable time to generalizing his theory even more. His last effort, the unified field theory, which was not entirely successful, was an attempt to understand all physical interactions—including electromagnetic interactions and weak and strong interactions—in terms of the modification of the geometry of space-time between interacting entities.
International Fame: After 1919, Einstein became internationally renowned. He accrued honors and awards, including the Nobel Prize in physics in 1921 from various world scientific societies. His visit to any part of the world became a national event; photographers and reporters followed him everywhere. While regretting his loss of privacy, Einstein capitalized on his fame to further his own political and social views.
Letter to FDR: Einstein sent a letter to President Roosevelt, pointing out the possibility of making an atomic bomb. In 1939 Einstein collaborated with several other physicists in writing a letter to President Franklin D. Roosevelt, pointing out the possibility of making an atomic bomb and the likelihood that the German government was embarking on such a course. The letter, which bore only Einstein’s signature, helped lend urgency to efforts in the U.S. to build the atomic bomb, but Einstein himself played no role in the work and knew nothing about it at the time.
Israel offers the Presidency: After the war, Einstein was active in the cause of international disarmament and world government. He continued his active support of Zionism but declined the offer made by leaders of the state of Israel to become president of that country. In the U.S. during the late 1940s and early ‘50s he spoke out on the need for the nation’s intellectuals to make any sacrifice necessary to preserve political freedom. Einstein died in Princeton on April 18, 1955.
Einstein Writings: Einstein’s efforts on behalf of social causes have sometimes been viewed as unrealistic. In fact, his proposals were always carefully thought out. Like his scientific theories, they were motivated by sound intuition based on a shrewd and careful assessment of evidence and observation. Although Einstein gave much of himself to political and social causes, science always came first, because he often said only the discovery of the nature of the universe would have lasting meaning. His writings include Relativity: The Special and General Theory (1916); About Zionism (1931); Builders of the Universe (1932); Why War? (1933), with Sigmund Freud; The World as I See It (1934); The Evolution of Physics (1938), with the Polish physicist Leopold Infeld; and Out of My Later Years (1950). Einstein’s collected papers are being published in a multi-volume work, beginning in 1987.
Scientists Create Matter Out of Light: Albert Einstein’s elegant equation E=mc2 predicted that energy could be converted to matter. Using a linear accelerator and high-energy laser light, physicists have done just that. Physicists at the Stanford Linear Accelerator Center (SLAC) in California have succeeded in producing particles of matter from very energetic collisions of light. The team, which included researchers from Stanford University, the University of Rochester in New York, the University of Tennessee in Knoxville, and Princeton University in New Jersey, published an account of their work in the September 1, 1997 issue of the journal Physical Review Letters.
Scientists have long known that matter can be converted to energy and, conversely, energy can be converted to matter. In 1905 physicist Albert Einstein quantified the relationship between matter and energy in his famous equation e=mc2, in which E is energy, m is mass, and c is the speed of light (300,000 km/sec [186,000 mi/sec]). In an atomic bomb blast, a very small amount of matter is converted to its equivalent in energy, creating an immense explosion.
Experiment to Confirm Einstein Theory: Scientists have also created matter from energy by bombarding heavy atoms (atoms made up of many protons and neutrons) with high-energy radiation in the form of X rays. Collisions between the X-ray beam and the atoms created matter in the form of sets of electron and positron particles, a phenomenon known as pair production. Positrons are particles that have the same weight and amount of charge as electrons, but positrons are positively charged, while electrons are negatively charged.
In the recent experiments at SLAC, physicists accelerated a beam of electrons to nearly the speed of light. They then aimed a split-second pulse of high-energy laser light directly at the electron beam. Occasionally a photon (a tiny, discrete unit of light energy) collided with an electron. The photon then recoiled from the collision and rebounded into oncoming photons from the laser beam with such violence that the resulting energy was converted into an electron-positron pair. Over several months of such experiments, the physicists were able to produce more than 100 electron-positron pairs.
Brownian Motion: Brownian motion is a constant erratic movement of tiny particles suspended in a fluid or gas. The phenomenon was discovered in 1827 by the British botanist Robert Brown. The inherent motion of the molecules of the fluid causes the molecules to strike the suspended particles at random. The impact makes the particles move. Albert Einstein in 1905 arrived at a mathematical explanation of the phenomenon and integrated it into kinetic theory. The French scientist Jean-Baptiste Perrin by a quantitative study of the Brownian motion made one of the earliest estimates of the value of Avogadro’s number.
Photoelectric Effect: Photoelectric Effect is a formation and liberation of electrically charged particles in matter when it is irradiated by light or other electromagnetic radiation. The term photoelectric effect designates several types of related interactions. In the external photoelectric effect, electrons are liberated from the surface of a metallic conductor by absorbing energy from light shining on the metal's surface. The effect is applied in the photoelectric cell, in which the electrons liberated from one pole of the cell, the photo-cathode, migrate to the other pole, the anode, under the influence of an electric field.
Study of the external photoelectric effect played an important role in the development of modern physics. Experiments beginning in 1887 showed that the external photoelectric effect had certain qualities that could not be explained by the theories of that time, in which light and all other electromagnetic radiation was considered to behave like waves. For example, as the light shining on a metal becomes increasingly intense, the classical wave theory of light suggests that the electrons that absorb the light will be liberated from the metal with more and more energy. However, experiments showed that the maximum possible energy of the ejected electrons depends only on the frequency of the incident light, and is independent of the light's intensity.
In 1905, in an effort to explain how the external photoelectric effect occurs, Albert Einstein suggested that light could be considered to behave like particles in some instances, and that the energy of each light particle, or photon, depends only on the wavelength of the light. To explain the external photoelectric effect, he envisioned light as a collection of projectiles hitting the metal. A free electron in the metal that is struck by a photon absorbs the photon's energy. If the photon is sufficiently energetic, the electron is dislodged from the metal. Einstein's theory explained many features of the external photoelectric effect, including why the maximum energy of electrons ejected from a metal is independent of the intensity of the incident light.
According to his theory, the maximum energy of a dislodged electron depends only on the energy with which a photon strikes the electron; the photon's energy, however, has nothing to do with the light intensity, because intensity only measures the number of photons striking the metal. The photon's energy, and thus the maximum possible energy of a dislodged electron, depends only on the light's frequency. Einstein's theory was later verified through further experimentation. His explanation of the photoelectric effect, with its demonstration that electromagnetic radiation can behave like a collection of particles in some situations, contributed to the development of quantum theory.
The term photoelectric effect can also refer to three other processes: Photo ionization, photoconduction, and the photovoltaic effect. Photo ionization is the ionization of a gas by light or other electromagnetic radiation; the photons must possess enough energy to detach one or more outer electrons from the gas atoms. In photoconduction, electrons in crystalline matter, by absorbing energy from photons, are brought to the range of energy levels at which they can move freely to conduct electricity. In the photovoltaic effect, photons create electron-hole pairs in semi conducting materials (see Semiconductor). In a transistor, this effect causes the formation of an electric potential across the junction between two different semiconductors in the transistor.
Planck’s Constant: Planck’s Constant is a fundamental physical constant, symbol h. It was first discovered (1900) by the German physicist Max Planck. Until that year, light in all forms had been thought to consist of waves. Planck noticed certain deviations from the wave theory of light on the part of radiations emitted by so-called blackbodies, or perfect absorbers and emitters of radiation. He came to the conclusion that these radiations were emitted in discrete units of energy, called quanta. This conclusion was the first enunciation of the quantum theory. According to Planck, the energy of a quantum of light is equal to the frequency of the light multiplied by a constant. His original theory has since had abundant experimental verification, and the growth of the quantum theory has brought about a fundamental change in the physicist's concept of light and matter, both of which are now thought to combine the properties of waves and particles.
Thus, Planck's constant has become as important to the investigation of particles of matter as to quanta of light, now called photons. The first successful measurement (1916) of Planck's constant was made by the American physicist Robert Millikan. The present accepted value of the constant is h = 6.626 × 10-34 joule-second in the meter-kilogram-second system.
Unified Field Theory: The Unified Field Theory, in physics, is a theory that proposes to unify the four known interactions, or forces—the strong, electromagnetic, weak, and gravitational forces—by a simple set of general laws. Four distinct forces are known to control all the observed interactions in matter: gravitation, electromagnetism, the strong force (a short-range force that holds atomic nuclei together), and the weak force (the force responsible for slow nuclear processes, such as beta decay). The attempts to develop a unified field theory are grounded in the belief that all physical phenomena should ultimately be explainable by some underlying unity.
One of the first to attempt the development of such a theory was Albert Einstein, whose work in relativity had led him to the hypothesis that it should be possible to find a unifying theory for the electromagnetic and gravitational forces. Einstein tried unsuccessfully during the last 30 years of his life to develop a theory that would represent forces and material particles by fields only, in which particles would be regions of very high field intensity. The development of quantum theory, which Einstein rejected, and the discovery of many new particles, however, precluded Einstein's success in formulating a unifying theory based on relativity and classical physics alone.
An important advance in this quest was made in 1967-68 by the American physicist Steven Weinberg and the Pakistani physicist Abdus Salam. They succeeded in unifying the weak interaction and the electromagnetic interaction by using a mathematical technique known as gauge symmetry (see Elementary Particles). According to this theory the electromagnetic interaction consists of the exchange of a photon and the weak interaction of the exchange of W and Z intermediate bosons. These bosons are believed to belong to the same family of particles as the photons.
Theoretical physicists are currently attempting to combine this so-called electro weak theory with the strong nuclear force, using symmetry theories; such attempts are known as grand unification theories (GUT). The effort also continues to combine all four fundamental interactions, including gravitation, in what are now known as super symmetry theories. Thus far, however, such attempts have not succeeded although they are proving useful in current work in cosmology (see Inflationary Theory).
Quantum Theory: Quantum Theory, in physics, is a description of the particles that make up matter and how they interact with each other and with energy. Quantum theory explains in principle how to calculate what will happen in any experiment involving physical or biological systems, and how to understand how our world works. The name “quantum theory” comes from the fact that the theory describes the matter and energy in the universe in terms of single indivisible units called quanta (singular quantum). Quantum theory is different from classical physics.
Classical physics is an approximation of the set of rules and equations in quantum theory. Classical physics accurately describes the behavior of matter and energy in the everyday universe. For example, classical physics explains the motion of a car accelerating or of a ball flying through the air.
Quantum theory, on the other hand, can accurately describe the behavior of the universe on a much smaller scale, that of atoms and smaller particles. The rules of classical physics do not explain the behavior of matter and energy on this small scale. Quantum theory is more general than classical physics, and in principle, it could be used to predict the behavior of any physical, chemical, or biological system. However, explaining the behavior of the everyday world with quantum theory is too complicated to be practical.
Most of Einstein’s colleagues felt that these efforts were misguided. Between 1915 and 1930 the mainstream of physics was in developing a new conception of the fundamental character of matter, known as quantum theory. This theory contained the feature of wave-particle duality (light exhibits the properties of a particle, as well as of a wave) that Einstein had earlier urged as necessary, as well as the uncertainty principle that states that precision in measuring processes is limited. Additionally, it contained a novel rejection, at a fundamental level, of the notion of strict causality. Einstein, however, would not accept such notions and remained a critic of these developments until the end of his life. “God,” Einstein once said, “does not play dice with the world.”
Uncertainty Principle: Uncertainty Principle, in quantum mechanics, is a theory stating that it is impossible to specify simultaneously the position and momentum of a particle, such as an electron, with precision. Also called the indeterminacy principle, the theory further states that a more accurate determination of one quantity will result in a less precise measurement of the other, and that the product of both uncertainties is never less than Planck's constant, named after the German physicist Max Planck. Of very small magnitude, the uncertainty results from the fundamental nature of the particles being observed. In quantum mechanics, probability calculations therefore replace the exact calculations of classical mechanics.
Formulated in 1927 by the German physicist Werner Heisenberg, the uncertainty principle was of great significance in the development of quantum mechanics. Its philosophic implications of indeterminacy created a strong trend of mysticism among scientists who interpreted the concept as a violation of the fundamental law of cause and effect. Other scientists, including Albert Einstein, believed that the uncertainty involved in observation in no way contradicted the existence of laws governing the behavior of the particles or the ability of scientists to discover these laws.
Einstein on Gravitation: After presenting his general theory of relativity in 1915, German-born American physicist Albert Einstein tried in vain to unify his theory of gravitation with one that would include all the fundamental forces in nature. Einstein discussed his special and general theories of relativity and his work toward a unified field theory in a 1950 Scientific American article. At the time, he was not convinced that he had discovered a valid solution capable of extending his general theory of relativity to other forces. He died in 1955, leaving this problem unsolved.
On the Generalized Theory of Gravitation: An account of the newly published extension of the general theory of relativity against its historical and philosophical background was requested by the Scientific American Publisher. It was a mathematical investigation concerning the foundations of field physics.
Some readers may be puzzled: Didn't we learn all about the foundations of physics when we were still at school? The answer is "yes" or "no," depending on the interpretation. We have become acquainted with concepts and general relations that enable us to comprehend an immense range of experiences and make them accessible to mathematical treatment. In a certain sense these concepts and relations are probably even final. This is true, for example, of the laws of light refraction, of the relations of classical thermodynamics as far as it is based on the concepts of pressure, volume, temperature, heat and work, and of the hypothesis of the non-existence of a perpetual motion machine.
What, then, impels us to devise theory after theory? Why do we devise theories at all?
The answer to the latter question is simply: Because we enjoy "comprehending," i.e., reducing phenomena by the process of logic to something already known or (apparently) evident. New theories are first of all necessary when we encounter new facts, which cannot be "explained" by existing theories. But this motivation for setting up new theories is, so to speak, trivial, imposed from without. There is another, more subtle motive of no less importance. This is the striving toward unification and simplification of the premises of the theory as a whole (i.e., Mach's principle of economy, interpreted as a logical principle).
There exists a passion for comprehension, just as there exists a passion for music. That passion is rather common in children, but gets lost in most people later on. Without this passion, there would be neither mathematics nor natural science. Time and again the passion for understanding has led to the illusion that man is able to comprehend the objective world rationally, by pure thought, without any empirical foundations—in short, by metaphysics. I believe that every true theorist is a kind of tamed metaphysics, no matter how pure a "positivist" he may fancy himself. The metaphysics believes that the logically simple is also the real. The tamed metaphysics believes that not all that is logically simple is embodied in experienced reality, but that the totality of all sensory experience can be "comprehended" on the basis of a conceptual system built on premises of great simplicity. The skeptic will say that this is a "miracle creed." Admittedly so, but it is a miracle creed which has been borne out to an amazing extent by the development of science.
The rise of atomism is a good example. How may Leucippus have conceived this bold idea? When water freezes and becomes ice—apparently something entirely different from water—why is it that the thawing of the ice forms something, which seems indistinguishable from the original water? Leucippus is puzzled and looks for an "explanation." He is driven to the conclusion that in these transitions the "essence" of the thing has not changed at all. Maybe the thing consists of immutable particles and the change is only a change in their spatial arrangement. Could it not be that the same is true of all material objects, which emerge again and again with nearly identical qualities?
This idea is not entirely lost during the long hibernation of occidental thought. Two thousand years after Leucippus, Bernoulli wonders why gas exerts pressure on the walls of a container. Should this be "explained" by mutual repulsion of the parts of the gas, in the sense of Newtonian mechanics? This hypothesis appears absurd, for the gas pressure depends on the temperature, all other things being equal. To assume that the Newtonian forces of interaction depend on temperature is contrary to the spirit of Newtonian mechanics. Since Bernoulli is aware of the concept of atomism, he is bound to conclude that the atoms (or molecules) collide with the walls of the container and in doing so exert pressure. After all, one has to assume that atoms are in motion; how else can one account for the varying temperature of gases?
A simple mechanical consideration shows that this pressure depends only on the kinetic energy of the particles and on their density in space. This should have led the physicists of that age to the conclusion that heat consists in random motion of the atoms. Had they taken this consideration as seriously as it deserved to be taken, the development of the theory of heat—in particular the discovery of the equivalence of heat and mechanical energy—would have been considerably facilitated.
This example is meant to illustrate two things. The theoretical idea (atomism in this case) does not arise apart from and independent of experience; nor can it be derived from experience by a purely logical procedure. It is produced by a creative act. Once a theoretical idea has been acquired, one does well to hold fast to it until it leads to an untenable conclusion.
As for my latest theoretical work, I do not feel justified in giving a detailed account of it before a wide group of readers interested in science. That should be done only with theories, which have been adequately confirmed by experience. So far it is primarily the simplicity of its premises and its intimate connection with what is already known (viz., the laws of the pure gravitational field) that speak in favor of the theory to be discussed here. It may, however, be of interest to a wide group of readers to become acquainted with the train of thought, which can lead to endeavors of such an extremely speculative nature. Moreover, it will be shown what kinds of difficulties are encountered and in what sense they have been overcome.
In Newtonian physics the elementary theoretical concept on which the theoretical description of material bodies is based is the material point, or particle. Thus matter is considered a priori to be discontinuous. This makes it necessary to consider the action of material points on one another as "action at a distance." Since the latter concept seems quite contrary to everyday experience, it is only natural that the contemporaries of Newton—and indeed Newton himself—found it difficult to accept. Owing to the almost miraculous success of the Newtonian system, however, the succeeding generations of physicists became used to the idea of action at a distance. Any doubt was buried for a long time to come. But when, in the second half of the 19th century, the laws of electrodynamics became known, it turned out that these laws could not be satisfactorily incorporated into the Newtonian system.
It is fascinating to muse: Would Faraday have discovered the law of electromagnetic induction if he had received a regular college education? Unencumbered by the traditional way of thinking, he felt that the introduction of the "field" as an independent element of reality helped him to coordinate the experimental facts. It was Maxwell who fully comprehended the significance of the field concept; he made the fundamental discovery that the laws of electrodynamics found their natural expression in the differential equations for the electric and magnetic fields. These equations implied the existence of waves, whose properties corresponded to those of light as far as they were known at that time.
This incorporation of optics into the theory of electromagnetism represents one of the greatest triumphs in the striving toward unification of the foundations of physics. Maxwell achieved this unification by purely theoretical arguments, long before it was corroborated by Hertz' experimental work. The new insight made it possible to dispense with the hypothesis of action at a distance, at least in the realm of electromagnetic phenomena. The intermediary field now appeared as the only carrier of electromagnetic interaction between bodies, and the field's behavior was completely determined by contiguous processes, expressed by differential equations.
Now a question arose: Since the field exists even in a vacuum, should one conceive of the field as a state of a "carrier," or should it rather be endowed with an independent existence not reducible to anything else? In other words, is there an "ether" which carries the field; the ether being considered in the undulatory state, for example, when it carries light waves?
The question has a natural answer: Because one cannot dispense with the field concept, it is preferable not to introduce in addition a carrier with hypothetical properties. However, the pathfinders who first recognized the indispensability of the field concept were still too strongly imbued with the mechanistic tradition of thought to accept unhesitatingly this simple point of view. But in the course of the following decades this view imperceptibly took hold.
The introduction of the field as an elementary concept gave rise to an inconsistency of the theory as a whole. Maxwell's theory, although adequately describing the behavior of electrically charged particles in their interaction with one another, does not explain the behavior of electrical densities, i.e., it does not provide a theory of the particles themselves. They must therefore be treated as mass points on the basis of the old theory. The combination of the idea of a continuous field with that of material points discontinuous in space appears inconsistent. A consistent field theory requires continuity of all elements of the theory, not only in time but also in space, and in all points of space. Hence the material particle has no place as a fundamental concept in a field theory. Thus even apart from the fact that gravitation is not included, Maxwell's electrodynamics cannot be considered a complete theory.
Maxwell's equations for empty space remain unchanged if the spatial coordinates and the time are subjected to a particular kind of linear transformations—the Lorentz transformations ("covariance" with respect to Lorentz transformations). Covariance also holds, of course, for a transformation, which is composed of two or more such transformations. This is called the "group" property of Lorentz transformations.
Maxwell's equations imply the "Lorentz group," but the Lorentz group does not imply Maxwell's equations. The Lorentz group may indeed be defined independently of Maxwell's equations as a group of linear transformations, which leave a particular value of the velocity—the velocity of light—invariant. These transformations hold for the transition from one "inertial system" to another, which is in uniform motion relative to the first. The most conspicuous novel property of this transformation group is that it does away with the absolute character of the concept of simultaneity of events distant from each other in space. On this account it is to be expected that all equations of physics are covariant with respect to Lorentz transformations (special theory of relativity). Thus it came about that Maxwell's equations led to a heuristic principle valid far beyond the range of the applicability or even validity of the equations themselves.
Special Relativity has this in Common with Newtonian Mechanics: The laws of both theories are supposed to hold only with respect to certain coordinate systems: those known as "inertial systems." An inertial system is a system in a state of motion such that "force-free" material points within it are not accelerated with respect to the coordinate system. However, this definition is empty if there is no independent means for recognizing the absence of forces. But such a means of recognition does not exist if gravitation is considered as a "field."
Let A be a system uniformly accelerated with respect to an "inertial system" I. Material points, not accelerated with respect to I, are accelerated with respect to A, the acceleration of all the points being equal in magnitude and direction. They behave as if a gravitational field exists with respect to A, for it is a characteristic property of the gravitational field that the acceleration is independent of the particular nature of the body. There is no reason to exclude the possibility of interpreting this behavior as the effect of a "true" gravitational field (principle of equivalence). This interpretation implies that A is an "inertial system," even though it is accelerated with respect to another inertial system. (It is essential for this argument that the introduction of independent gravitational fields is considered justified even though no masses generating the field are defined. Therefore, to Newton such an argument would not have appeared convincing.) Thus the concepts of inertial system, the law of inertia and the law of motion are deprived of their concrete meaning—not only in classical mechanics but also in special relativity. Moreover, following up this train of thought, it turns out that with respect to A time cannot be measured by identical clocks; indeed, even the immediate physical significance of coordinate differences is generally lost.
In view of all these difficulties, should one not try, after all, to hold on to the concept of the inertial system, relinquishing the attempt to explain the fundamental character of the gravitational phenomena, which manifest themselves in the Newtonian system as the equivalence of inert and gravitational mass?
Those who trust in the comprehensibility of nature must answer: No. This is the gist of the principle of equivalence: In order to account for the equality of inert and gravitational mass within the theory it is necessary to admit non-linear transformations of the four coordinates. That is, the group of Lorentz transformations and hence the set of the "permissible" coordinate systems has to be extended.
What group of coordinate transformations can then be substituted for the group of Lorentz transformations? Mathematics suggests an answer which is based on the fundamental investigations of Gauss and Riemann: namely, that the appropriate substitute is the group of all continuous (analytical) transformations of the coordinates. Under these transformations the only thing that remains invariant is the fact that neighboring points have nearly the same coordinates. The coordinate system expresses only the topological order of the points in space (including its four-dimensional character). The equations expressing the laws of nature must be covariant with respect to all continuous transformations of the coordinates. This is the principle of general relativity.
The procedure just described overcomes a deficiency in the foundations of mechanics, which had already been noticed by Newton and was criticized by Leibnitz and, two centuries later, by Mach. Inertia resists acceleration, but acceleration relative to what? Within the frame of classical mechanics the only answer is: Inertia resists acceleration relative to space. This is a physical property of space—space acts on objects, but objects do not act on space. Such is probably the deeper meaning of Newton's assertion spatium est absolutum (space is absolute). But the idea disturbed some, in particular Leibnitz, who did not ascribe an independent existence to space but considered it merely a property of "things" (contiguity of physical objects). Had his justified doubts won out at that time, it hardly would have been a boon to physics, for the empirical and theoretical foundations necessary to follow up his idea were not available in the 17th century.
According to general relativity, the concept of space detached from any physical content does not exist. The physical reality of space is represented by a field whose components are continuous functions of four independent variables—the coordinates of space and time. It is just this particular kind of dependence that expresses the spatial character of physical reality.
Since the theory of general relativity implies the representation of physical reality by a continuous field, the concept of particles or material points cannot play a fundamental part, nor can the concept of motion. The particle can only appear as a limited region in space in which the field strength or the energy density is particularly high.
A relativistic theory has to answer two questions: 1) What is the mathematical character of the field? 2) What equations hold for this field? Concerning the first question: From the mathematical point of view the field is essentially characterized by the way its components transform if a coordinate transformation is applied. Concerning the second question: The equations must determine the field to a sufficient extent while satisfying the postulates of general relativity. Whether or not this requirement can be satisfied depends on the choice of the field-type.
The attempt to comprehend the correlations among the empirical data on the basis of such a highly abstract program may at first appear almost hopeless. The procedure amounts, in fact, to putting the question: What most simple property can be required from what most simple object (field) while preserving the principle of general relativity? Viewed from the standpoint of formal logic, the dual character of the question appears calamitous, quite apart from the vagueness of the concept "simple." Moreover, from the standpoint of physics there is nothing to warrant the assumption that a theory, which is “logically simple”, should also be "true."
Yet every theory is speculative. When the basic concepts of a theory are comparatively "close to experience" (e.g., the concepts of force, pressure, mass), its speculative character is not so easily discernible. If, however, a theory is such as to require the application of complicated logical processes in order to reach conclusions from the premises that can be confronted with observation, everybody becomes conscious of the speculative nature of the theory. In such a case an almost irresistible feeling of aversion arises in people who are inexperienced in epistemological analysis and who are unaware of the precarious nature of theoretical thinking in those fields with which they are familiar.
On the other hand, it must be conceded that a theory has an important advantage if its basic concepts and fundamental hypotheses are "close to experience," and greater confidence in such a theory is certainly justified. There is less danger of going completely astray, particularly since it takes so much less time and effort to disprove such theories by experience. Yet more and more, as the depth of our knowledge increases, we must give up this advantage in our quest for logical simplicity and uniformity in the foundations of physical theory. It has to be admitted that general relativity has gone further than previous physical theories in relinquishing "closeness to experience" of fundamental concepts in order to attain logical simplicity. This holds already for the theory of gravitation, and it is even truer of the new generalization, which is an attempt to comprise the properties of the total field.
In the generalized theory the procedure of deriving from the premises of the theory conclusions that can be confronted with empirical data is so difficult that so far no such result has been obtained. In favor of this theory are, at this point, its logical simplicity and its "rigidity." Rigidity means here that the theory is either true or false, but not modifiable.
The greatest inner difficulty impeding the development of the theory of relativity is the dual nature of the problem, indicated by the two questions we have asked. This duality is the reason why the development of the theory has taken place in two steps so widely separated in time. The first of these steps, the theory of gravitation, is based on the principle of equivalence discussed above and rests on the following consideration: According to the theory of special relativity, light has a constant velocity of propagation. If a light ray in a vacuum starts from a point, designated by the coordinates x1, x2 and x3 in a three dimensional coordinate system, at the time x4, it spreads as a spherical wave and reaches a neighboring point (x1 + dx1, x2 + dx2, x3 + dx3) at the time x4 + dx4.
Introducing the velocity of light, c, we write the
expression:
v(dx12+dx22+dx32)=cdx4
This can also be written in the form:
dx12+dx22+dx32-c2 dx42=0
This expression represents an objective relation between neighboring space-time points in four dimensions, and it holds for all inertial systems, provided the coordinate transformations are restricted to those of special relativity. The relation loses this form, however, if arbitrary continuous transformations of the coordinates are admitted in accordance with the principle of general relativity. The relation then assumes the more general form:
Sik gik dxi dxk=0
The gik are certain functions of the coordinates, which transform in a definite way if a continuous coordinate transformation is applied. According to the principle of equivalence, these gik functions describe a particular kind of gravitational field: a field, which can be obtained by transformation of "field-free" space. The gik satisfy a particular law of transformation. Mathematically speaking, they are the components of a "tensor" with a property of symmetry, which is preserved in all transformations; the symmetrical property is expressed as follows:
gik=gki
The idea suggests itself: May we not ascribe objective meaning to such a symmetrical tensor, even though the field cannot be obtained from the empty space of special relativity by a mere coordinate transformation? Although we cannot expect that such a symmetrical tensor will describe the most general field, it may well describe the particular case of the "pure gravitational field." Thus it is evident what kind of field, at least for a special case, general relativity has to postulate: a symmetrical tensor field.
Hence only the second question is left: What kind of general covariant field law can be postulated for a symmetrical tensor field?
This question has not been difficult to answer in our time, since the necessary mathematical conceptions were already at hand in the form of the metric theory of surfaces, created a century ago by Gauss and extended by Riemann to manifolds of an arbitrary number of dimensions. The result of this purely formal investigation has been amazing in many respects. The differential equations, which can be postulated as field law for gik, cannot be of lower than second order, i.e., they must at least contain the second derivatives of the gik with respect to the coordinates. Assuming that no higher than second derivatives appear in the field law, it is mathematically determined by the principle of general relativity. The system of equations can be written in the form:
Rik=0
The Rik transforms in the same manner as the gik, i.e.; they too form a symmetrical tensor.
These differential equations completely replace the Newtonian theory of the motion of celestial bodies provided the masses are represented as singularities of the field. In other words, they contain the law of force as well as the law of motion while eliminating "inertial systems."
The fact that the masses appear as singularities indicate that these masses themselves cannot be explained by symmetrical gik fields, or "gravitational fields." Not even the fact that only positive gravitating masses exist can be deduced from this theory. Evidently a complete relativistic field theory must be based on a field of more complex nature, that is, a generalization of the symmetrical tensor field. Before considering such a generalization, two remarks pertaining to gravitational theory are essential for the explanation to follow.
The first observation is that the principle of general relativity imposes exceedingly strong restrictions on the theoretical possibilities. Without this restrictive principle it would be practically impossible for anybody to hit on the gravitational equations, not even by using the principle of special relativity, even though one knows that the field has to be described by a symmetrical tensor. No amount of collection of facts could lead to these equations unless the principle of general relativity was used. This is the reason why all attempts to obtain a deeper knowledge of the foundations of physics seem doomed to me unless the basic concepts are in accordance with general relativity from the beginning. This situation makes it difficult to use our empirical knowledge, however comprehensive, in looking for the fundamental concepts and relations of physics, and it forces us to apply free speculation to a much greater extent than is presently assumed by most physicists.
I do not see any reason to assume that the heuristic significance of the principle of general relativity is restricted to gravitation and that the rest of physics can be dealt with separately on the basis of special relativity, with the hope that later on the whole may be fitted consistently into a general relativistic scheme. I do not think that such an attitude, although historically understandable, can be objectively justified. The comparative smallness of what we know today as gravitational effects is not a conclusive reason for ignoring the principle of general relativity in theoretical investigations of a fundamental character. In other words, I do not believe that it is justifiable to ask: What would physics look like without gravitation?
The second point we must note is that the equations of gravitation are 10 differential equations for the 10 components of the symmetrical tensor gik. In the case of a non-general relativistic theory, a system is ordinarily not over determined if the number of equations is equal to the number of unknown functions. The manifold of solutions is such that within the general solution a certain number of functions of three variables can be chosen arbitrarily. For a general relativistic theory this cannot be expected as a matter of course. Free choice with respect to the coordinate system implies that out of the 10 functions of a solution, or components of the field, four can be made to assume prescribed values by a suitable choice of the coordinate system.
In other words, the principle of general relativity implies that the number of functions to be determined by differential equations is not 10 but 10-4=6. For these six functions only six independent differential equations may be postulated. Only six out of the 10 differential equations of the gravitational field ought to be independent of each other, while the remaining four must be connected to those six by means of four relations (identities). And indeed there exist among the left-hand sides, Rik, of the 10 gravitational equations four identities—“Bianchi's identities"—, which assure their "compatibility."
In a case like this—when the number of field variables is equal to the number of differential equations—compatibility is always assured if the equations can be obtained from a variation principle. This is indeed the case for the gravitational equations.
However, the 10 differential equations cannot be entirely replaced by six. The system of equations is indeed "over determined," but due to the existence of the identities it is over determined in such a way that its compatibility is not lost, i.e., the manifold of solutions is not critically restricted. The fact that the equations of gravitation imply the law of motion for the masses is intimately connected with this (permissible) over determination.
After this preparation it is now easy to understand the nature of the present investigation without entering into the details of its mathematics. The problem is to set up a relativistic theory for the total field. The most important clue to its solution is that there exists already the solution for the special case of the pure gravitational field. The theory we are looking for must therefore be a generalization of the theory of the gravitational field. The first question is: What is the natural generalization of the symmetrical tensor field?
This question cannot be answered by itself, but only in connection with the other question: What generalization of the field is going to provide the most natural theoretical system? The answer on which the theory under discussion is based is that the symmetrical tensor field must be replaced by a non-symmetrical one. This means that the condition gik=gki for the field components must be dropped. In that case the field has 16 instead of 10 independent components.
There remains the task of setting up the relativistic differential equations for a non-symmetrical tensor field. In the attempt to solve this problem one meets with a difficulty, which does not arise in the case of the symmetrical field. The principle of general relativity does not suffice to determine completely the field equations, mainly because the transformation law of the symmetrical part of the field alone does not involve the components of the ant symmetrical part or vice versa. Probably this is the reason why this kind of generalization of the field has hardly ever been tried before. The combination of the two parts of the field can only be shown to be a natural procedure if in the formalism of the theory only the total field plays a role, and not the symmetrical and ant symmetrical parts separately.
It turned out that this requirement can indeed be satisfied in a natural way. But even this requirement, together with the principle of general relativity, is still not sufficient to determine uniquely the field equations. Let us remember that the system of equations must satisfy a further condition: the equations must be compatible. It has been mentioned above that this condition is satisfied if the equations can be derived from a variation principle.
This has indeed been achieved, although not in so natural a way as in the case of the symmetrical field. It has been disturbing to find that it can be achieved in two different ways. These variation principles furnished two systems of equations—let us denote them by E1 and E2—which were different from each other (although only slightly so), each of them exhibiting specific imperfections. Consequently even the condition of compatibility was insufficient to determine the system of equations uniquely.
It was, in fact, the formal defects of the systems E1 and E2 that indicated a possible way out. There exists a third system of equations, E3, which is free of the formal defects of the systems E1 and E2 and represents a combination of them in the sense that every solution of E3 is a solution of E1 as well as of E2. This suggests that E3 may be the system we have been looking for. Why not postulate E3, then, as the system of equations? Such a procedure is not justified without further analysis, since the compatibility of E1 and that of E2 do not imply compatibility of the stronger system E3, where the number of equations exceeds the number of field components by four.
An independent consideration shows that irrespective of the question of compatibility the stronger system, E3, is the only really natural generalization of the equations of gravitation.
But E3 is not a compatible system in the same sense as are the systems E1 and E2, whose compatibility is assured by a sufficient number of identities, which means that every field that satisfies the equations for a definite value of the time has a continuous extension representing a solution in four-dimensional space. The system E3, however, is not extensible in the same way. Using the language of classical mechanics we might say: In the case of the system E3 the "initial condition" cannot be freely chosen. What really matters is the answer to the question: Is the manifold of solutions for the system E3 as extensive as must be required for a physical theory? This purely mathematical problem is as yet unsolved.
The skeptic will say: "It may well be true that this system of equations is reasonable from a logical standpoint. But this does not prove that it corresponds to nature." You are right, dear skeptic. Experience alone can decide on truth. Yet we have achieved something if we have succeeded in formulating a meaningful and precise question. Affirmation or refutation will not be easy, in spite of an abundance of known empirical facts. The derivation, from the equations, of conclusions, which can be confronted with experience, will require painstaking efforts and probably new mathematical methods.
Understanding the Universe
Quotations of Albert Einstein
(1879-1955): There are a total of forty-five quotations by Dr. Albert
Einstein.
"Einstein predicted the bending of starlight in the vicinity of a massive body such as the sun."
“God,” Einstein once said, “does
not play dice with the world.”
"As far as the laws of
mathematics refer to reality, they are not certain; and as far as they are
certain, they do not refer to reality."
"Before God we are all
equally wise - and equally foolish."
"Do not worry about your
difficulties in Mathematics. I can assure you mine are still greater."
"Ethical axioms are found and
tested not very differently from the axioms of science. Truth is what stands
the test of experience."
"Few people are capable of
expressing with equanimity opinions which differ from the prejudices of their
social environment. Most people are
even incapable of forming such opinions."
"I know not with what weapons
World War III will be fought, but World War IV will be fought with sticks and
stones."
"I never think of the future
- it comes soon enough."
"If I had only known, I would
have been a locksmith."
"If you are out to describe
the truth, leave elegance to the tailor."
"Imagination is more
important than knowledge…"
"Laws alone cannot secure
freedom of expression. In order that
every man present his views without penalty there must be spirit of tolerance
in the entire population."
"My religion consists of a
humble admiration of the illimitable superior spirit who reveals himself in the
slight details we are able to perceive with our frail and feeble mind."
"Only two things are
infinite, the universe and human stupidity, and I'm not sure about the
former."
"Reading, after a certain
age, diverts the mind too much from its creative pursuits. Any man who reads too much and uses his own
brain too little falls into lazy habits of thinking."
"Reality is merely an
illusion, albeit a very persistent one."
"The ideals which have
lighted my way, and time after time have given me new courage to face life
cheerfully, have been Kindness, Beauty, and Truth. The trite subjects of human efforts, possessions, outward
success, luxury have always seemed to me contemptible."
"The important thing is not
to stop questioning. Curiosity has its own reason for existing. One cannot help
but be in awe when he contemplates the mysteries of eternity, of life, of the
marvelous structure of reality. It is
enough if one tries merely to comprehend a little of this mystery every day.
Never lose a holy curiosity."
"The most beautiful thing we
can experience is the mysterious. It is the source of all true art and
science."
"The most incomprehensible
thing about the world is that it is at all comprehensible."
"The release of atomic energy
has not created a new problem. It has merely made more urgent the necessity of
solving an existing one."
"The secret to creativity is
knowing how to hide your sources."
"To punish me for my contempt
for authority, fate made me an authority myself."
"Too many of us look upon
Americans as dollar chasers. This is a cruel libel, even if it is reiterated
thoughtlessly by the Americans themselves."
"Truth is what stands the
test of experience."
"Try not to become a man of
success but rather to become a man of value."
"We should take care not to
make the intellect our god; it has, of course, powerful muscles, but no
personality."
"Yes, we have to divide up
our time like that, between our politics and our equations. But to me our equations are far more
important, for politics are only a matter of present concern. A mathematical equation stands
forever."
"Science without religion is
lame; religion without science is blind."
"Everything that is really
great and inspiring is created by the individual who can labor in
freedom."
"It is the duty of every
citizen according to his best capacities to give validity to his convictions in
political affairs."
"Common sense is the
collection of prejudices acquired by age eighteen."
"Everything should be made as
simple as possible, but not one bit simpler."
"If the facts don't fit the
theory, change the facts."
"Insanity: doing the same
thing over and over again and expecting different results."
"Not everything that can be
counted counts, and not everything that counts can be counted."
"The hardest thing in the
world to understand is the income tax."
"The significant problems we
have cannot be solved at the same level of thinking with which we created them."
"You cannot simultaneously
prevent and prepare for war."
"If A is success in life,
then A equals x plus y plus z. Work is
x; y is play; and z is keeping your mouth shut."
"Great spirits have always
encountered opposition from mediocre minds.
The mediocre mind is incapable of understanding the man who refuses to
bow blindly to conventional prejudices and chooses instead to express his
opinions courageously and honestly."
"The unleashed power of the
atom has changed everything save our modes of thinking and we thus drift toward
unparalleled catastrophe."
"When you look at yourself
from a universal standpoint, something inside always reminds or informs you
that there are bigger and better things to worry about."
"You see, wire telegraph is a
kind of a very, very long cat. You pull
his tail in New York and his head is meowing in Los Angeles. Do you understand this? And radio operates exactly the same way: you
send signals here, they receive them there.
The only difference is that there is no cat."
Tributes to Albert Einstein: With his brilliant theoretical work, German-born American physicist Albert Einstein single-handedly revolutionized 20th-century physics and opened up many new branches of scientific research. In this 1955 article from Scientific American, Nobel-laureate physicists Niels Bohr of Denmark and Isidor Isaac Rabi of the United States paid tribute to Einstein and discussed the importance of his contributions to physics.
Albert Einstein: 1879-1955
By Niels Bohr and I. I. Rabi
With the death of Albert Einstein, a life in the service of science and humanity, which was as rich and fruitful as any in the whole history of our culture, has come to an end. Mankind will always be indebted to Einstein for the removal of the obstacles to our outlook, which were involved, in the primitive notions of absolute space and time. He gave us a world picture with a unity and harmony surpassing the boldest dreams of the past.
Einstein's genius, characterized equally by logical clarity and creative imagination, succeeded in remolding and widening the imposing edifice whose foundations had been laid by Newton's great work. Within the frame of the relativity theory, demanding a formulation of the laws of nature independent of the observer and emphasizing the singular role of the speed of light, gravitational effects lost their isolated position and appeared as an integral part of a general kinematic description, capable of verification by refined astronomical observations. Moreover, Einstein's recognition of the equivalence of mass and energy should prove an invaluable guide in the exploration of atomic phenomena.
Indeed, the breadth of Einstein's views and the openness of his mind found most remarkable expression in the fact that, in the very same years when he gave a widened outlook to classical physics, he thoroughly grasped the fact that Planck's discovery of the universal quantum of action revealed an inherent limitation in such an approach. With unfailing intuition Einstein was led to the introduction of the idea of the photon as the carrier of momentum and energy in individual radioactive processes. He thereby provided the starting point for the establishment of consistent quantum theoretical methods, which have made it possible to account for an immense amount of experimental evidence concerning the properties of matter, and even demanded reconsideration of our most elementary concepts.
The same spirit that characterized Einstein's unique scientific achievements also marked his attitude in all human relations. Notwithstanding the increasing reverence which people everywhere felt for his attainments and character, he behaved with unchanging natural modesty and expressed himself with a subtle and charming humor. He was always prepared to help people in difficulties of any kind, and to him, who himself had experienced the evils of racial prejudice, the promotion of understanding among nations was a foremost endeavor. His earnest admonitions on the responsibility involved in our rapidly growing mastery of the forces of nature will surely help to meet the challenge to civilization in the proper spirit.
To the whole of mankind Albert Einstein's death is a great loss, and to those of us who had the good fortune to enjoy his warm friendship it is a grief that we shall never more be able to see his gentle smile and listen to him. But the memories he has left behind will remain an ever-living source of fortitude and encouragement. —Niels Bohr
With Albert Einstein's death a great light has gone out in the world of physics, for Einstein, more than any other man, set the tone of the physics of the 20th century. His theories of special and general relativity were the capstone of classical physics and the theory of fields. His theory of light quanta and his later demonstration of the nature of the fluctuations of "black body" radiation raised the paradox of the wave-particle duality, which was partly resolved two decades later in the principle of complementarily of Niels Bohr and Werner Heisenberg. His 1917 paper, introducing the ideas of spontaneous and stimulated emission of radiation, was the first clear statement of the statistical nature of fundamental atomic phenomena.
The famous Einstein A and B coefficients led to the quantitative use of the correspondence principle and to the formulation of the Kramer’s-Heisenberg dispersion formula, which in turn led to Heisenberg's matrix mechanics. Einstein was therefore in a very real sense the founder of the statistical theory of fundamental atomic phenomena.
There is scarcely any important fundamental idea in modern physics whose origin does not trace back at least in part to Einstein. Yet, like many another father, he was not really satisfied with the children of his scientific imagination. He never regarded his mighty contributions to quantum theory as other than provisional suggestions for the ordering of phenomena. The subsequent formulations of quantum mechanics and especially the thoroughgoing statistical interpretations were to him philosophically and esthetically repugnant.
The Einstein-Bose statistics and the Einstein condensation phenomenon were his last important positive contributions to quantum theory. His subsequent role with respect to quantum theory was that of a critic. He applied the force of his great imagination to the construction of imaginary experiments, which involved the theory in seemingly paradoxical and contradictory predictions. The resolution of these paradoxes, chiefly through the efforts of Bohr, served to refine and clarify the principle of complementarily but left Einstein unconvinced.
His real love was the theory of fields, which he pursued with unremitting vigor to the very end of his more than 50 years of active scientific life. This preoccupation is to a large degree the key to his scientific personality. The theory of general relativity was constructed on the basis of a physical observation of the equivalence of inertial and gravitational mass under certain simple circumstances. Beyond that, his guiding principles were his esthetic and philosophical urge for simplicity and symmetry. His intuition and taste led him to believe that the equivalence principle was true in general, and that the equations of physics must be covariant in all systems of coordinates. With these guidelines and with the use of mathematical tools already at hand, he built a theory of gravitation and of the structure of the cosmos.
Like a mystic who has had a divine illumination, Einstein in his search for the ideal could be satisfied with nothing less than a theory, which would encompass all phenomena—atomic and cosmic. He once remarked to me in a discussion concerning the newly discovered meson: "We already know that the electron is quantized in charge and mass. Should not this be enough empirical information for a theory of matter?" It was a goal of this grandeur that drove him in his search for a unified field theory.
Einstein was a unique personality. He was not attracted by fame or fortune nor swayed by the opinions of the majority. He knew his talent and guarded it jealously against outside interference. Although fearless in support of any cause he considered worthy, he gave only so much of himself and no more. Physics was his life, and he lived it according to his own lights, with complete objectivity and integrity.
He was the prince of physicists, and the imprint of his mighty strides will give direction to his beloved science for generations to come.
Einstein in Hollywood: American playwright George S. Kaufman gleefully satirizes the Hollywood studio system in this 1938 spoof. His fictional premise is that Warner Brothers Pictures, Inc., is collaborating with physicist Albert Einstein on a motion picture about Einstein’s theory of relativity.
“Einstein in Hollywood”
August 6, 1938
By George S. Kaufman
Warner Brothers have cabled Sigmund Freud, in London, asking him to come to Hollywood to assist in the preparation of the new Bette Davis picture, Dark Victory. Sigmund Freud had been in Hollywood about a year, and was engaged to marry Merle Oberon, when the studio got another great idea. Louella Parsons broke the story, and her papers gave it a two-column heading:
Warner Brothers to Film Theory of Relativity. Professor
Einstein Signed to Write Screen Treatment of Own Story—Arrives in Hollywood
Next Month.
Einstein's arrival in Hollywood, of course, was the signal for a gay round of dinners and cocktail parties. The Basil Rathbones, who had given a party in Freud's honor to which everyone came as his favorite neurosis, gave one for Einstein in which the guests were got up as their favorite numbers. Needless to say, there were some pretty hot numbers. The climax, however, was a dinner at the Trocadero, given by the film colony as a whole, at which Will H. Hays was the principal speaker. "The signing of Professor Einstein for pictures," said Mr. Hays," is the greatest forward step that the industry has ever taken. American motion pictures appeal to people all over the world. I will be happy to okay Professor Einstein's contract just as soon as we get permission from Germany."
Next morning, on the Warner lot, Professor Einstein was assigned an office in the writers' building and a stenographer named Goldie. Promptly at twelve o'clock he was summoned to a conference.
The producer received him with a flourish. "Professor," he said, "allow me to introduce Sol Bergen and Al Jenkins, who are going to work with you on the picture. Now, I've been thinking this thing over, and we want this to be absolutely your picture. What you say goes. But of course we all want a hit, and I'm sure you're willing to play ball with us. Now, I've got some great news for you. I've decided to put Joan Blondell in it." Sol Bergen let out a war whoop. "Gee, Boss, that's great. Her name alone will put it over." "I want the Professor to have the best," said the producer, "because I'm sure he's going to give us a great picture. Now, Professor, here's the problem: how can we treat this theory of yours so as to keep it just as you wrote it—because this has got to be your picture—and still make it entertainment? Because first and foremost a motion picture has got to be entertainment. But of course we want your theory in it too."
"I'm not sure that I've got the Professor's theory exactly straight," said Al Jenkins. "Would you mind, Professor, giving me just a quick summary of it, in a sort of non-technical way?" "I don't think we have to bother the Professor about that," said the producer. "I've been thinking it over, and I've got a great way to work it in. And here it is." He leaned back and looked at them. "The scene is a college where they teach this theory of the Professor's. Only it's a very tough theory, and there's never been a girl that's been able to understand it. Of course it's a co-ed college. And finally along comes a girl, attractive, of course, and says, 'I am going to understand it.'" "Blondell!" said Sol Bergen.
"Right!" said the producer. "So she pitches in and goes to work. She won't go to parties or dances or anything, and she wears horn-rimmed glasses, and the boys think she's a grind and hasn't got any sex appeal. Underneath, of course, she's a regular girl."
"There's got to be one guy in particular that falls for her," said Jenkins.
"Sure!" said the producer, "and I'll tell you who'd be great in the part. Wayne Morris. How's that, Professor? How'd you like to have Wayne Morris in your picture?"
"Let's make him the captain of the football team," said Bergen. "It'll give us a great finale."
"Fine!" said the producer. "Now, Blondell has got a girl friend that goes to college with her, only she's a different type. Flighty, and never does any studying, but a smart little kid when it comes to handling the boys. Knows 'em from A to Z. Now, there's a millionaire, an old grad that's just presented the college with a stadium, and his son is going to the college. Lots of money, and a racing car, and this kid set her cap for him. We could have a crack-up on his way back from the roadhouse." "Or else he could lead the college band," said Bergen. "That way you get your music in." "Great! And we have a kid playing the girl that can handle a couple of numbers. Here's an idea, Professor. How about Warren and Dubin for the score? How would you like that, huh?" "And how's this?" asked Jenkins. "She has another girl friend that sort of likes the older boys—with dough, see? And she sets out after the rich father." "I've got it!" said the producer. "I've got the title! 'Gold Diggers at College.' Yes, sir, 'Gold Diggers at College,' by Albert Einstein, Sol Bergen, and Al Jenkins, based on the Theory of Relativity, by Albert Einstein. Professor, you've done a great picture!"
Summary: Albert Einstein began
his school career in Munich. He did not
talk until the age of three, but even as a youth he showed a brilliant
curiosity about nature and an ability to understand difficult mathematical
concepts. At the age of 12 he taught
himself Euclidean geometry. He studied
the violin from the age 6 to 13. He
studied mathematics, in particular calculus, beginning around 1891.
In 1895 Einstein failed an examination that would have allowed him to
study for a diploma as an electrical engineer at the Eidgenössische Technische
Hochschule in Zurich. Einstein renounced German citizenship in 1896 and was to
be stateless for a number of years. He
did not even apply for Swiss citizenship until 1899; citizenship being granted
in 1901. In 1902 he secured a position
as an examiner in the Swiss patent office in Bern.
During World War I he was one of a handful of German academics willing
to publicly decry Germany’s involvement in the war. Einstein made his first visit to the United States in 1922. Einstein received the Nobel Prize in 1921
but not for relativity rather for his 1905 work on the photoelectric
effect. Among further honors that
Einstein received were the Copley Medal of the Royal Society in 1925 and the
Gold Medal of the Royal Astronomical Society in 1926.
A third visit to the United States in
1932 was followed by the offer of a post at Princeton. The idea was that
Einstein would spend seven months a year in Berlin, five months at
Princeton. Einstein accepted and left
Germany in December 1932 for the United States. The following month the Nazis
came to power in Germany and Einstein was never to return there. In 1940 Einstein became a citizen of the
United States, but also chose to retain his Swiss citizenship. In 1944 he made a contribution to the war
effort by hand writing his 1905 paper on special relativity and putting it up for
auction. It raised six million dollars,
the manuscript today being in the Library of Congress.
After the death of the first president of Israel in 1952, the Israeli
government decided to offer the post of second president to Einstein. One week before his death Einstein signed
his last letter. It was a letter to
Bertrand Russell in which he agreed that his name should go on a manifesto
urging all nations to give up nuclear weapons.
Although brought up as the son of "entirely irreligious (Jewish) parents,"
through the teaching in his Catholic primary school, mixed with his private
instruction in elements of the Jewish religion, Einstein found within himself a
"deep religiosity"– indeed, "the religious paradise of youth.
Inserting the cosmological constant in the relativity equation was the
biggest blunder of his life. In the
first of three seminal papers that were published in 1905, Einstein examined
the phenomenon discovered by Max
Planck. In 1905 Albert Einstein published his
special theory of relativity. A very
small amount of matter is equivalent to a vast amount of energy. For example, 1 kg (2.2 lb) of matter
converted completely into energy would be equivalent to the energy released by
exploding 22 megatons of TNT. He sent a
letter to FDC to suggest to develop the atomic bomb as Germany had plans to
develop such a weapon .
Bibliography
TIME 100: Person of the Century -
Albert Einstein Collection of articles from Time Magazine portrays Einstein as
the greatest mind of the 20th century. www.time.com/time/time100/
poc/magazine/albert_einstein5a.html Mar
25, 2005.
Albert Einstein Quotes - The
Quotations Page. Albert Einstein, "Science, Philosophy and Religion: a
Symposium", 1941 ...
www.quotationspage.com/quotes/Albert_Einstein.
Quick Facts about Einstein,
Microsoft ® Encarta ® Reference Library 2004. © 1993-2003 Microsoft
Corporation. All rights reserved.
Quotes of Albert Einstein
(1879-1955), web site:
http://www.quotationspage.com/quotes/Albert_Einstein/31.
X-Ray Experiment to confirm
Einstein Theory of Relativity: Source: Encarta Yearbook, September 1997.
Microsoft ® Encarta ® Reference Library 2004. © 1993-2003 Microsoft
Corporation. All rights reserved.
Brownian Motion, Microsoft ® Encarta ® Reference Library
2004. © 1993-2003 Microsoft Corporation. All rights reserved.
Photoelectric effect, Microsoft ®
Encarta ® Reference Library 2004. © 1993-2003 Microsoft Corporation. All rights
reserved.
Planck's constant, Microsoft ®
Encarta ® Reference Library 2004. © 1993-2003 Microsoft Corporation. All rights
reserved.
Unified Fieold Theory, Microsoft ®
Encarta ® Reference Library 2004. © 1993-2003 Microsoft Corporation. All rights
reserved.
Quantum Theory contributed by
Contributed By: Samuel Glasstone, Microsoft ® Encarta ® Reference Library 2004.
© 1993-2003 Microsoft Corporation. All rights reserved.
Uncertainty Principle, Microsoft ®
Encarta ® Reference Library 2004. © 1993-2003 Microsoft Corporation. All rights
reserved.
Tribute to Albert Einstein,
(1879-1955),contributed by By Niels Bohr and I. I. Rabi,
Microsoft ® Encarta ® Reference
Library 2004. © 1993-2003 Microsoft Corporation. All rights reserved.
Letter to FDR, Albert Einstein
Source: Library of Congress.
Microsoft ® Encarta ® Reference
Library 2004. © 1993-2003 Microsoft Corporation. All rights reserved.
“Einstein in Hollywood”, August 6,
1938 By George S. Kaufman, Microsoft ® Encarta ® Reference Library 2004. ©
1993-2003 Microsoft Corporation. All rights reserved.
Source: Kaufman, George S.
“Einstein in Hollywood.” The Nation, August 6, 1938. Microsoft ® Encarta ®
Reference Library 2004. © 1993-2003 Microsoft Corporation. All rights reserved.
Archive Photos; Culver Pictures, Inc. Einstein: Scientist
and Activist, Microsoft ® Encarta ® Reference Library
2004. © 1993-2003 Microsoft Corporation. All rights reserved.
Albert Einstein Biography
Article by: J J O'Connor and E F Robertson,
April 1997, Microsoft ® Encarta ®
Reference Library 2004. © 1993-2003 Microsoft Corporation. All rights reserved.
Scientific Works of
Albert Einstein, web site: http://www.humboldt1.com/~gralsto/einstein/scien.html
A correspondence between
Albert Einstein and Sigmund Freud, web
site:
http://www.wordit.com/why/why_war.html
As the World as I
see it by Albert Einstein, web site: http://www.aip.org/history/einstein/essay.htm
Einstein Third
Paradise by Gerald Horton, web site: http://www.aip.org/history/einstein/essay-einsteins-third-
paradise.htm
Einstein Time by
Peter Gallison, web site: http://www.aip.org/history/einstein/essay-einsteins-time.htm