January 25, 2006

Scientific Report

The Effects of the Coriolis on the Environment

By Frank J. Collazo

Introduction: The Coriolis Effects was chosen as the topic for the project because the equation is used to correct errors due to the earth’s rotation to major strategic weapon systems. The effect is well heralded among industrialized nations producing strategic weaponry. The correction is necessary to compensate for the rotation of the earth in navigation, ballistic trajectories, understanding of hurricanes and their trajectories for prediction, and most of all, solar navigation by birds.

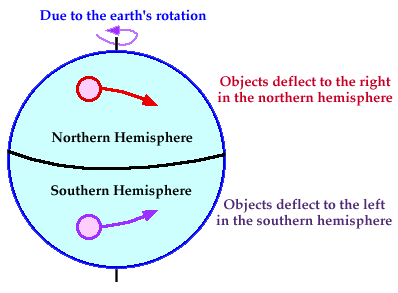
In the northern hemisphere, the Corolis Effect causes moving objects and currents to be deflected to the right; in the southern hemisphere it causes deflection to the left. 

As air begins to flow from high to low pressure, the Earth rotates under it making the wind follow a curved path. In the Northern Hemisphere, the wind turns to the right of its direction of motion. In the Southern Hemisphere, it turns to the left. The Coriolis force is zero at the equator.

Gaspard de Coriolis

The effect is named after its discoverer, French mathematician Gaspard de Coriolis (1792–1843).

Coriolis Force: Coriolis Force and Coriolis Acceleration, in mechanics, are additional forces or accelerations acting on the motion of bodies in a rotating system of reference. For example, an object moving above the Earth in a generally northerly or southerly direction, and with a constant velocity relative to space, will be deflected in relation to the rotation of Earth. This deflection is clockwise in the northern hemisphere and counterclockwise in the southern hemisphere. The effect is named after the French physicist Gaspard de Coriolis, who first analyzed the phenomenon mathematically. Coriolis forces are of considerable importance in determining prevailing winds and ocean currents and also in the analysis of the flight paths of missiles and rockets.

The science of meteorology benefited from advances in other sciences, technology, and mathematics. In 1660 Irish-born English scientist Robert Boyle discovered the relationship between pressure and volume of a gas. English meteorologist George Hadley, in 1735, used physics and mathematics to explain how the earth’s rotation influences the trade winds in the tropics. By flying a kite in a thunderstorm in 1752, American statesman and scientist Benjamin Franklin demonstrated the electrical nature of lightning. French chemist Jacques Charles, in 1787, discovered the relationship between temperature and volume in a gas. In 1835 French physicist Gaspard de Coriolis mathematically demonstrated the effect that the earth’s rotation has on atmospheric motions.

The Coriolis Force is an artifact of the earth's rotation. Once air has been set in motion by the pressure gradient force, it undergoes an apparent deflection from its path, as seen by an observer on the earth. This apparent deflection is called the "Coriolis Force" and is a result of the earth's rotation.

As air moves from high to low pressure in the northern hemisphere, it is deflected to the right by the Coriolis force. In the southern hemisphere, air moving from high to low pressure is deflected to the left by the Coriolis force.

The amount of deflection the air makes is directly related to both the speed at which the air is moving and its latitude. Therefore, slowly blowing winds will be deflected only a small amount, while stronger winds will be deflected more. Likewise, winds blowing closer to the poles will be deflected more than winds at the same speed closer to the equator. The Coriolis Force is zero right at the equator.

Pressure Gradient Force: The Pressure Gradient Force is directed from high to low pressure. The change in pressure measured across a given distance is called a "pressure gradient."

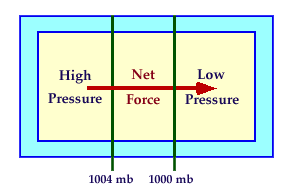
The pressure gradient results in a net force that is directed from high to low pressure, and this force is called the "pressure gradient force."

High Pressure Centers are also known as anticyclones. A high-pressure center is where the pressure has been measured to be the highest relative to its surroundings. That means, moving in any direction away from the "High" will result in a decrease in pressure. A high-pressure center also represents the center of an anticyclone and is indicated on a weather map by a blue "H."

Low Pressure Centers are also known as cyclones. A low-pressure center is where the pressure has been measured to be the lowest relative to its surroundings. That means, moving in any horizontal direction away from the "Low" will result in an increase in pressure. Low-pressure centers also represent the centers of cyclones.

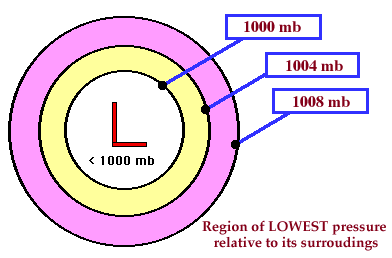
A low pressure center is indicated on a weather map by a red "L" and winds flow counterclockwise around a low in the northern hemisphere. The opposite is true in the southern hemisphere, where winds flow clockwise around an area of low pressure.

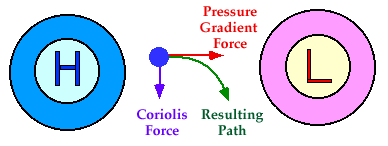
Geotropic Wind: Winds balanced by the Coriolis and pressure gradient forces. An air parcel initially at rest will move from high pressure to low pressure because of the Pressure Gradient Force (PGF). However, as that air parcel begins to move, it is deflected by the Coriolis force to the right in the northern hemisphere (to the left on the southern hemisphere). As the wind gains speed, the deflection increases until the Coriolis force equals the pressure gradient force. At this point, the wind will be blowing parallel to the isobars. When this happens, the wind is referred to as geotropic.

The movie below illustrates the process mentioned above, while the diagram at right shows the two forces balancing to produce the geotropic wind. Winds in nature are rarely exactly geotropic, but to a good approximation, the winds in the upper troposphere can be close. This is because winds are only considered truly geotropic when the isobars are straight and there are no other forces acting on it -- and these conditions just aren't found too often in nature.

Secrets of Animal Navigation: In 1942 Henry L. Yeagley, a Pennsylvania State College physicist, proposed that a homing pigeon could tune into the earth’s magnetic field and, simultaneously, sense the effect of the earth’s rotation on its flight path—the Coriolis effect, named after the French engineer who described it. Yeagley argued that magnetic and Coriolis information would create a “navigational grid work” akin to lines of latitude and longitude, thus supplying the two coordinates for position finding. Yeagley’s experiments were dismissed by those who thought it farfetched that a pigeon could sense the earth’s rotation. “Though Yeagley didn't really prove his case, history is showing that he was asking the right questions,” says Kreithen, who agrees that a pigeon might sense the earth's rotation. “People on a revolving disk detect rotations as slow as one every 2.4 hours. That's just an order of magnitude away from detecting the rotation of the earth. So it's not unreasonable to ask if an animal has that ability.”

James Gould comments: “Given the contradictory results we get in pigeon studies, we probably should go out and do Yeagley’s experiments again. “At the turn of the century,” Gould continues, “we assumed that animals were color-blind, and it was an incredible shock for some of us to learn that bees had color vision. Later on we discovered that fish could hear, pigeons could see ultraviolet light, and snakes have an infrared sensing apparatus. “The whole history of animal behavior is the animals taking us by surprise,” says Gould. “Why shouldn't they have some surprises for us now?”

Solar Navigation by Birds: There has been considerable argument about how pigeons find their home roosts. Mechanisms involving the sun's altitude, the sun's change of altitude, Coriolis forces, and terrestrial magnetism have all been proposed to explain this phenomenon. The technique of taking birds away from the roost, releasing them, and estimating their direction of departure is expensive, inaccurate, and inconclusive.

A recent technique of operant training used by A. Whiten of the University of Bristol overcomes these problems. The birds were trained to peck keys arranged in a circle around them and were rewarded when they pecked the key that pointed toward home. Therefore, when the birds were taken north, they pecked the south-facing key. When the birds were taken north—but the apparent altitude of the sun was changed to that of a position south of home by means of a prism—the birds reacted as if they had been taken south. Then, in the laboratory the birds considered home, artificial suns were set up with arcs corresponding to solar arcs visible at positions away from home; the birds reacted as if they had been moved from home to the spots indicated by the artificial suns. In this way, Whiten demonstrated the importance of solar position in the homing behavior of pigeons.

How the pigeons perceive and use this solar information is not clear, but a fairly accurate clock is required. Pigeons can also navigate in overcast conditions, but their performance is seriously affected by altering the magnetic field, as William Keeton of Cornell University has shown. Even in sunny conditions, inexperienced pigeons or pigeons released far from home are upset if magnets are glued to their backs. So it is likely that pigeons use a variety of cues in their homing, with the importance of each depending on the weather conditions.

Trade Winds: The trade winds are a major part of the general circulation pattern of the earth’s atmosphere. They blow from a high-pressure belt near 30° latitude in each hemisphere, called a subtropical high, toward a low-pressure belt near the equator called the equatorial low. In the equatorial low the air rises and travels aloft to the subtropical highs, where it then sinks. Because of the apparent deflecting force of the earth’s rotation, known as the Coriolis force, the trade winds do not blow due south or due north toward the equator. Instead, they blow from the northeast in the northern hemisphere and from the southeast in the southern hemisphere. The entire trade wind belt system moves about 5° of latitude northward during summer (July) and southward during winter (December).

Giant Ocean Cataracts: The study of real-world cataracts must take into account the fact that oceans contain many basins. Certain complicating factors that I shall discuss below, such as the Coriolis force and friction, also enter the picture, with the result that the paths of some cataracts are not oriented from north to south and do not end at the Equator. Nevertheless, the simple model accounts for most of the observations: cataracts of cold, dense water flow from the polar basins into the temperate-latitude basins. At each stage the water is warmed through skimming and mixing. Thus the bottom temperature of ocean basins increases toward the Equator.

Understanding the Coriolis Force: The Coriolis force does influence long-lasting vortices. Pressure differences tend to push winds in straight paths. Yet winds follow curved paths across the Earth. In 1835, Gustave-Gaspard Coriolis, a French scientist, first described mathematically what's going on, giving his name to the Coriolis force.

In simple terms, as air begins flowing from high to low pressure, the Earth rotates under it, making the wind follow a curved path. In the Northern Hemisphere, the wind turns to the right of its direction of motion. In the Southern Hemisphere, it turns to the left. The Coriolis force is zero at the equator.

You might be wondering: If the Coriolis force turns winds to the right in the Northern Hemisphere, then why do winds go counterclockwise around large systems such as hurricanes north of the equator?

This happens because Coriolis is only one of the forces acting on air to cause winds. In simple terms, in the Northern Hemisphere, while the Coriolis force is pushing the wind toward the right, the pressure-gradient force, caused by air pressure differences, is pushing the air toward the center of the area of low pressure and for various reasons is stronger then the Coriolis force.

Flush this nonsense down the drain. Don't believe what you hear about Coriolis making the water in a sink or toilet rotate one way as it drains in one hemisphere, the other way in the other hemisphere. The Coriolis force is noticeable only for large-scale motions such as winds. The winds move counterclockwise around storms in the Northern Hemisphere while the Coriolis force pushes moving objects to the right, and why it is correct to call it the "Coriolis force," instead of the "Coriolis effect."

Coriolis Force and Hurricanes: The fact that the Coriolis force is zero at the equator and very weak near the equator, explains why tropical cyclones such as hurricanes and typhoons won't form on the equator even though the other factors there, such as warm ocean water, would make them likely. But, the idea that you don't have to worry about tropical cyclones in the zone about 180 miles north and south of the equator isn't a sure thing.

Tropical Storm: The rotation of the Earth also affects the movement of air. In the northern hemisphere, Earth’s rotation deflects air from left to right, while in the southern hemisphere, it deflects air from right to left. This deflection is called the Coriolis effect (see Coriolis Force). As air moves toward a low-pressure center, the deflection causes the air to spiral around the center rather than travel straight into the center. The inward spiraling of air causes the formation of circular bands of thunderstorms, which are a distinctive feature of tropical storms and hurricanes, along with spiraling winds. The spiraling winds rotate faster as they approach the center. Centrifugal force flings the rotating air outward, making it increasingly difficult for air to reach the center (see Centripetal Force).

Coriolis Effect on Missile Trajectory: The Coriolis force only operates on objects traveling in a north-south direction; and it really is the latitudinal differences in easterly component that causes the behavior. In fact, the magnitude of the Coriolis force is independent of the direction in which something is moving. If you were to present your example as if it were an explanation of the Coriolis force, you are now stuck with its inability to handle the behavior of a missile as it goes similarly off track after being fired in an easterly or westerly direction.

Things Attributed to the Coriolis Force: Factors attributed to the earth’s rotation: The direction of rotation that arises out of the rocking motion of Celts (known commercially as rattle backs). Its shape, in fact, determines the interesting motion of Celts.

In the 1945 movie, Adventure, the Clark Gable character apparently points out that ringlets in a women’s hair curl in one direction in the Northern Hemisphere, the opposite direction in the Southern hemisphere!

The spiraling hooks with which vines cling to their supports are asserted (incorrectly) to change from one hemisphere to the other.

The direction dog’s turn before lying down has been claimed to be dependent upon the hemisphere in which they live.

"Getting Around The Coriolis Force"

Introduction and Motivation: At some point in their lives, most people hear about the Coriolis force, whether in reference to weather patterns, sea currents or, most prosaically, which way water flows down the sink. Unfortunately, while many have heard of it, few understand it well enough to explain it without resorting to vector equations.

Of course, most physics textbooks, which deal with angular kinematics will have the following equation relating the Coriolis force to an object's mass (m), its velocity in a rotating frame (v_r) and the angular velocity of the rotating frame of reference:

F_Coriolis = -2 m ( x v_r)

The text will then either explain the Coriolis force in terms of angular quantities such as conservation of angular momentum, or will use the Coriolis force to illustrate the angular kinematics. Unfortunately, most of us are not comfortable with angular mechanics. It would not be an exaggeration to say that some students dread it. Nor can we expect students to enter the classroom understanding the Coriolis force. Hence, whether using physics to explain the phenomenon or using the phenomenon to explain the physics, students are shaky on both sides of this relationship.

So, what to do? This article intends to develop a means of explaining the Coriolis effect to people who haven't yet grasped angular mechanics. The explanation relies on linear quantities and uses rotational concepts infrequently.

The Basic Premises: The following principles are needed before starting the body of the explanation.

Newton's First Law in component form - Objects in motion stay in motion unless acted on by an unbalanced force. A vector component of velocity will not be changed by a force perpendicular to that component.

Spherical Geometry of the Earth - X degrees of longitude gives you different distances between longitude lines (in miles or kilometers) at different latitudes, plus a few additional results of being on a sphere which will be detailed later.

Gravity - Objects under the influence of Earth's gravity will fall towards (and thus orbit) the center of mass of the Earth.

Force - In one way of looking at it, a force is anything that causes a mass to accelerate in one's frame of reference. However, most people think of force as "something doing something to something." The Coriolis effect is a force in the first sense, but not in the second sense: nothing is actually pushing or pulling on anything, the acceleration is due to the fact that the observer is moving in a circle. From this point on, the Coriolis effect will not be directly called a force, even though that's how it's normally characterized.

Note: Premise 2 is probably the easiest to accept since you can draw on a globe to demonstrate that an inch is 15 degrees of longitude at one latitude and 30 degrees at another. Having a ball or globe on hand for the explanation is generally helpful. Premises 1 and 3 require some science background, however, but should be acceptable to students in mechanics courses.

Explanation of the Coriolis Effect: While all Coriolis-based deflection can be explained using rotational concepts, a linear explanation is simpler if you separate the effects into those in the north/south direction and those in the east/west direction. The deflection of objects moving north and south can be explained without invoking centripetal acceleration, as we see next.

The Earth Moves Under My Feet: North/South Motion: Note first that all points on the Earth have the same rotational velocity, the earth goes around once per day. Also, places at different latitudes have different linear speeds. A point near the equator may go around a thousand miles in an hour, while one near the North Pole could be moving only a few dozen miles in an hour.

Normally, objects in contact with the ground travel the same speed as the ground they stand on. As a result, the Coriolis effect generally doesn't have a noticeable effect to people on the ground; the speed of the point you're standing on and the speed of the point you're stepping onto are too close for you to tell the difference. Or, looking back at the Coriolis effect equation above, if the velocity relative to the rotating frame (the Earth) is zero, so is the Coriolis effect.

However, when an object moves north or south and is not firmly connected to the ground (air, artillery fire, etc), then it maintains its initial eastward speed as it moves. This is just an application of Newton's First Law. An object moving east continues going east at that speed (both direction and magnitude remain the same) until something exerts a force on it to change its velocity. Objects launched to the north from the equator retain the eastward component of velocity of other objects sitting at the equator. But if they travel far enough away from the equator, they will no longer be going east at the same speed as the ground beneath them.

The result is that an object traveling away from the equator will eventually be heading east faster than the ground below it and will seem to be moved east by some mysterious "force." Objects traveling towards the equator will eventually be going more slowly than the ground beneath them and will seem to be forced west. In reality there is no actual force involved; the ground is simply moving at a different speed than its original "home ground" speed, which the object retains.

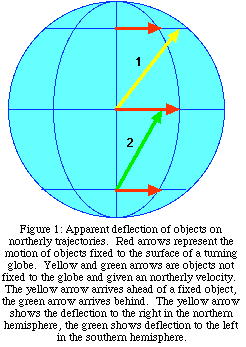
Consider Figure 1. Yellow arrow 1 represents an object sent north from the equator. By the time it reaches the labeled northern latitude, it has traveled farther east than a similar point on the ground at that latitude has, since it kept the eastward speed it had when it left the equator. Similarly, green arrow 2 started south of the equator at a slower eastward speed, and doesn't go as far east as the ground at the equator...seeming to deflect west from the point of view of the ground.

It Used To Be East/West Motion: In explaining how the Coriolis effect acts on objects moving to the east or west, it helps to turn off gravity for a moment. Don't worry, we'll turn it back on later, just be sure to put the lid back on your coffee.
Consider being on a rotating sphere with no gravity. An observer who is glued to the sphere throws a ball straight to the "east" on the globe, in the direction of rotation. Since there are no forces on the ball, it will travel in a straight line, the tangent line shown in Figure 2 at t=0.

Time passes, and the ball continues on its straight line. But the observer is attached to the globe and moves around to a new position. At this new position, the observer's definition of the "east" direction has changed, and is no longer the same as it was at time t=0. The ball is no longer traveling on the observer's "east" line, and, in fact, seems to have drifted off to one side. If the globe is spinning slowly enough that the observer can't feel the spin, then the natural conclusion would be that some mysterious force pushed the ball off course, sending it drifting away from the axis of rotation more quickly than it would go if it were still heading the "correct" easterly direction.

Similarly, if the observer throws a ball to the west at time t=0, it will seem to have been forced inward towards the axis of rotation because the "west" line has moved. Now to turn gravity back on. Gravity pulls objects towards the center of mass of the Earth, which means it cannot change an object's velocity in the directions perpendicular to up and down. In other words, it won't change the east/west or north/south components of an object's velocity.

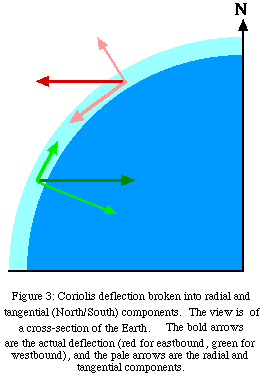Figure 3 states there is a slice through the Earth. The eastbound projectile would seem to drift away from the axis, while the westbound projectile would seem to drift towards the axis. Both of these lines have been split into components, with one component being "up/down" and the other being "north/south." Gravity will act against any "up" components, and the presence of the ground will act against any "down" components, so projectiles will stay within the "atmosphere."

As a result of gravity pulling down on objects and the ground holding them up, the remaining effect of the Coriolis effect on objects heading east or west is to deflect them to the north or south. In the northern hemisphere, objects heading east are deflected to the south, for example. The Coriolis effect "pushes" them away from the axis, and gravity pulls the object back down to the ground so that the remaining effect is an apparent "push" to the south.

It's worth noting that this effect is weakest at the equator, since there are no north/south components to "great circle" motion moving east or west along the equator. And, of course, it's also weakest at the poles, since there's no meaningful east or west motion. It turns out that this effect is strongest at mid-latitudes.

Low Pressure Systems: Now we've explained how things moving towards the poles curve to the east, things moving away from the poles curve to the west, things moving east curve towards the equator, and things moving west curve towards the poles. In other words, air (or anything else) moving freely in the northern hemisphere deflect to the right, air moving freely in the southern hemisphere deflect to the left. And this is what the result of the vector cross products in the Coriolis effect equation says as well, in its mathematical shorthand.

What does this mean for, say, weather systems? Take, for example, a low-pressure center where there's less air than in the area around it. If there's less air in one place than in the surroundings, air will try to move in to balance things out.

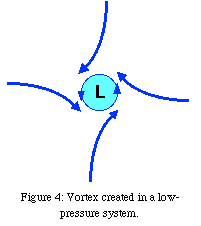
Air starting at rest with respect to the ground will move towards a low-pressure center. Such motion in the Northern Hemisphere will deflect to its right, as shown in Figure 4. However, the forces that got the air moving towards the low-pressure center in the first place are still around, and the result will be a vortex of air spinning counter-clockwise. Air will try to turn to the right, the low-pressure system will try to draw the air into itself, and the result is that air is held into a circle that actually turns to the left. Without the Coriolis effect, fluid rushing in towards a point could still form a vortex, but the direction would either be random or depend solely on the initial conditions of the fluid.

The eye of a hurricane is a clear example of fast winds bent into a tight circle, moving so fast that they can't be "pulled in" to the center. The very low pressure at the center of the hurricane means that there is a strong force pulling air towards the center, but the high speed of the wind invokes the Coriolis effect strongly enough that the forces reach a kind of balance. The net force on air at the eye wall is a centripetal force large enough to keep the air out at a given radius determined by its speed.

Other Results and Non-Results:  "Fine," you may say, "that explains storms. But what about water going down the sink?” In fact, this question is a good "hook" for getting students interested in the Coriolis effect in the first place.

Because the Earth's angular velocity is so small (360 degrees per day, or about 7 x 10^-5 radians per second) the Coriolis effect isn't really significant over small distances (as equation 1 shows). High velocity also can make a difference, but for the purposes of this paper small distance-high speed effects will not be considered. So, what things are likely to be affected by the Coriolis effect in a large way?

Up in the Air:  Just looking at a weather system on the nightly news gives one example that has already been addressed. Large weather systems feature masses of air and moisture that travel hundreds of miles and can have wind speeds reaching over a hundred miles an hour in the worst storms.

Another example of a quickly moving object in the sky, which covers hundreds of miles, is an airplane. All pilots need to have familiarity with the effects of the Coriolis effect, since airplanes can reach speeds much higher than even the fastest hurricane winds. Over the course of a several hour trip, an airplane could be deflected by a significant amount if the pilot did not compensate for the Coriolis effect.

Long-distance artillery may or may not be another example of something requiring a Coriolis correction. I have seen some papers that say it is negligible compared to the Magnus force (a result of the fact artillery shells spin) and others that claim it is important on its own.

What about Water Going the Wrong Way Down the Sink: In a kitchen sink, of course, speeds and time scales are much smaller than hours and miles. Water rushing down a drain flows at speeds on the order of a meter per second in most sinks that are less than a meter wide. Qualitatively, there doesn't seem to be much chance for deflection. Putting these numbers into Equation 1 results in an estimated change in rotation of only a fraction of a degree per second, and a very small fraction at that...less than an arc-second (1/3600th of a degree) per second over the course of the entire draining of the sink, ignoring additional effects caused by conservation of angular momentum and the like.

Under extremely controlled conditions, this can cause water to flow out of a container counter-clockwise in the northern hemisphere and clockwise in the southern hemisphere, but your kitchen sink is not so controlled. Things like leftover spin from filling the sink (even when the water looks still, it's rotating slowly for a long time after it seems to stop) irregularities in the construction of the basin, convection currents if the water is warmer or colder than the basin, and so forth, can affect the direction water goes down the sink. Any one of these factors is usually more than enough to overwhelm the small contribution of the Coriolis effect in your kitchen sink or bathtub. Research in the 1960s showed that if you do carefully eliminate these factors, the Coriolis effect can be observed.

Water in the sink doesn't go far enough to trigger a noticeable north/south deflection. Most often, it simply spirals down the sink the way it went into the sink, and the same is true of things like the famous "demonstration" of the Coriolis effect shown at tourist traps along the Equator (especially since east/west deflection is absent). Maybe there is a conspiracy to manufacture right-handed sinks in the Northern Hemisphere and left-handed sinks in the Southern Hemisphere? In any case, do not blame it on the Coriolis effect unless your sink is the size of a small ocean.

Coriolis Effect Equation: In physics, the Coriolis effect is an inertial force first described by Gaspard Gustave Coriolis, a French scientist in 1835. When the equations of motion are formulated in a rotating coordinate system, a term arises which looks like a force called the Coriolis force.

In changing from an essentially inertial coordinate system (such as the "frame of the fixed stars") to a rotating frame of reference (such as that of the Earth's surface) a term appears in the equation of motion described by the formula: Where bold indicates vector quantities, m is mass, v is the velocity and Ω is the angular velocity of the coordinate system. Note that this equation ignores the second-order term in Ω, which in geophysical terms is small and can anyway be absorbed into the gravitational potential term.

This equation means that the force will be proportional to the velocity of the object and the rotation of the coordinate system. The force will be in a direction perpendicular to the velocity (and thus does no work). If an object is traveling on earth in the northern hemisphere, the Coriolis force will deflect the object to the right. In the southern hemisphere the reverse is true, while at the equator the horizontal component of the force is zero for horizontal motions. For instance, the effect breaks up the atmospheric circulation from atmospheric circulation of the tropics to the polar regions into a series of cells in which the surface winds have a prevailing eastward or westward component.

The Coriolis force plays a strong role in weather patterns, where it affects prevailing winds and the rotation of storms, as well as in the direction of ocean currents. Above the atmospheric boundary layer, friction plays a relatively minor role, as air parcels move mostly parallel to each other. Here, an approximate balance between pressure gradient force and Coriolis force exists, causing the geotropic wind, which is the wind effected by these two forces only to blow along isobars (along lines of constant geopotential height, to be precise). Thus a northern hemispheric low-pressure system rotates in a counterclockwise direction, while northern hemispheric high-pressure systems or cyclones on the southern hemisphere rotate in a clockwise manner, as described by Buys-Ballors Law.

.

The Coriolis effect must also be considered in astronomy and stellar dynamic, where it affects phenomena such as the rotational direction of sunspots. The flight paths of airplanes, artillery shells, and missiles must account for the Coriolis effect or risk being off course by significant amounts.

The Coriolis effect can also be observed in the motion of a simple pendulum. For instance, if a pendulum is set swinging at the North pole, the pendulum will oscillate in a fix plane while the earth rotates beneath it. Hence for an observer on earth, the plane of oscillation would appear to rotate once a day. This effect is present at other latitudes although the oscillations are more complicated but the phenomenon is qualitatively the same.

Foucault's Pendulum: Named after the French physicist Jean Foucalt, it was conceived as an experiment to demonstrate the rotation of the Earth and the Coriolis Effect. It is a tall pendulum free to oscillate in any vertical plane and capable of running for many hours, and was first exhibited in 1851 from the ceiling of the Pantheon in Paris.

At almost any location on Earth -- except the equator -- it can be observed that the plane within which the pendulum swings slowly rotates. At either the North Pole or South Pole, the plane of oscillation of a pendulum rotates once per sidereal day (in essence, the pendulum remains in the same plane while the Earth rotates underneath it, as predicted by Newton’s first Law of motion). At other latitudes, the plane of oscillation of a pendulum rotates with an angular speed proportional to the sine of its latitude; thus one at 45° rotates once every 1.4 days and one at 30° every 2 days.

Another classical instance where the Coriolis force produces a measurable effect is in the deflection of falling object. Hence, in the northern hemisphere, a body falling freely is deflected to the east.

Although the Coriolis force is relatively small and does not have an observable influence on small systems such as the whirlpool of a draining bathtub, toilet or sink, the Coriolis effect can have a visible effect over large amounts of time and has been observed to cause uneven wear on railroad tracks and cause rivers to dig their beds deeper on one side.

Mass Flow Meter: A practical application of the Coriolis force is the mass flow meter, an instrument that measures the mass flow rate of a fluid through a tube. The instrument was introduced in 1977 by Micro Motion Inc. Simple flow meters measure volume flow rate, which is proportional to mass flow rate only when the density of the fluid is constant. If the fluid has varying density, or contains bubbles, then the volume flow rate multiplied by the density is not an accurate measure of the mass flow rate.

The Coriolis mass flow meter works by applying a vibrating force to a curved tube through which the fluid passes. The Coriolis effect creates a force on the tube perpendicular to both the direction of vibration and the direction of flow. This force is measured to give the mass flow rate. Coriolis flow meters can also be used with non-Newtonian fluids, which tend to give inaccurate results with volume flow meters. The same instrument can be used to measure the density of the fluid, since this affects the resonant frequency of the vibrating tube.

A further advantage of this instrument is that the fluid is contained in a smooth tube, with no moving parts that would need to be cleaned and maintained, and that would impede the flow. Effects due to the Coriolis force also appear in atomic physics. In polyatomic molecules, the molecule motion can be described by a rigid body rotation and internal vibration of atoms about their equilibrium position. As a result of the vibrations of the atoms, the atoms are in motion relative to the rotating coordinate system of the molecule. A Coriolis force is therefore present and will cause the atoms to move into a direction perpendicular to the original oscillations. This leads to a mixing in molecular spectra between the rotational and vibration levels.

Is the Coriolis Force "Fictitious?" It is common to see the Coriolis force described as "making it look like a force is acting upon the object, but actually there is no real force acting on the object." This prompts the question, "what is a real force?" From the viewpoint of General Relativity, all coordinate systems are equivalent in describing physical processes, but in changing from one system to another things that look like forces will arise. For example, at the surface of Earth it is possible to (locally) remove the gravitational force by changing to a coordinate system accelerating towards the center of Earth. But none would call gravity "fictitious."

Buys-Ballot's Law: Buys-Ballot's law, in meteorology, is the name given to a law which may be expressed as follows: In the Northern Hemisphere, stand with your back to the wind; the low pressure area will be on your left. In other words, wind travels counter clockwise around low-pressure zones in the Northern Hemisphere. It is approximately true in the higher latitudes of the Northern Hemisphere, and is reversed in the southern Hemisphere, but the angle between barometric gradient and wind is not a right angle in low latitudes.

Because of the Earth’s spherical shape and its rotation, the planet’s centrifugal force and the Coriolis effect affect weather. When a low-pressure system develops, air from the north and south of the low-pressure area must flow into it. In the Northern Hemisphere, air further to the south is traveling faster because it is closer to the equator and therefore further from the Earth's axis of rotation, which means it travels further in a day (rotational period) than the air to the north of it. When that air from the south is drawn north into a low pressure system, it will be moving faster than the ground below it, since that northern ground has slower eastward motion than the ground to the south.

So as the southern air moves north, it will also move east due to its higher speed. Similarly, the air to the north is moving slower than the air to the south. So when the air from the north is forced south toward the low-pressure system, it lags behind the ground in the south, causing it to also move west. Of course, the low-pressure system will continue to draw the air, which causes it to swirl around the low-pressure area in a counterclockwise direction. In the Southern Hemisphere this is reversed, and the air swirls in a clockwise direction.

Coriolis Effect Related to Meteorology: The tendency for any moving body on or above the earth’s surfaces, e.g., an ocean current or an artillery round, is to drift sideways from its course because of the earth's rotation. In the Northern Hemisphere the deflection is to the right of the motion; in the Southern Hemisphere it is to the left. The Coriolis deflection of a body moving toward the north or south results from the fact that the earth's surface is rotating eastward at greater speed near the equator than near the poles, since a point on the equator traces out a larger circle per day than a point on another latitude nearer either pole.

A body traveling toward the equator with the slower rotational speed of higher latitudes tends to fall behind or veer to the west relative to the more rapidly rotating earth below it at lower latitudes. S similarly, a body traveling toward either pole veers eastward because it retains the greater eastward rotational speed of the lower latitudes as it passes over the more slowly rotating earth closer to the pole. It is extremely important to account for the Coriolis effect when considering projectile trajectories, terrestrial wind systems, and ocean currents.

Cloud Formation: As air rises, it is a good approximation that the parcel cools adiabatically. Vertical motion is so rapid that as the air expands no heat exchange occurs between the particle and its surroundings. Condensation occurs when the air reaches saturation. Water droplets form on condensation nuclei and for the purposes of this study, this shall be assumed to happen when the air reaches 100% humidity. It shall also be assumed that there is a sufficient concentration of condensation nuclei for condensation to occur. In an adiabatic expansion, the ratio of temperature of the air, T, the pressure, P, the specific heat capacity at constant pressure, Cp, and R, the gas constant, holds as below:

T/P Raised to the Power R/Cp=B: This derives from the first law of thermodynamics and using the definitions of specific heat capacity and constant volume and at constant pressure. The temperature at which air reaches a relative humidity of 100% depends upon the total water content or absolute humidity of the air parcel as can be seen from the chart below in Figure 1.

This derives from the first law of thermodynamics and using the definitions of specific heat capacity and constant volume and at constant pressure. The temperature at which air reaches a relative humidity of 100% depends upon the total water content or absolute humidity of the air parcel as can be seen from the chart below in Figure 1.

Dynamic Atmosphere: The temperature differences produced by inequalities in heating cause differences in air density and pressure that propel the winds. Vertical air motions are propelled by buoyancy: A region of air that is warmer and less dense than the surroundings is buoyant and rises. Air is also forced from regions of higher pressure to regions of lower pressure. Once the air begins moving, it is deflected by the Coriolis force, which results from the earth’s rotation. The Coriolis force deflects the wind and all moving objects toward their right in the northern hemisphere and toward their left in the southern hemisphere. It is so gentle that it has little effect on small-scale winds that last less than a few hours, but it has a profound effect on winds that blow for many hours and move over large distances.

Coriolis Effect on Hurricanes: The Coriolis Effect is not really much of an effect at all. Also known as the Coriolis Force, this term is just used to define why a hurricane spins.

When the hurricane travels, it is actually moving in a straight line. It appears to move in a curve because the earth is moving underneath it.

In the northern hemisphere, hurricanes rotate in a counterclockwise direction, whereas in the southern hemisphere it moves clockwise. Why? The earth’s surface is rotating eastward at a greater speed near the equator than near the two poles. Storms traveling toward the equator will veer to the west because it falls behind to the moving earth. Storms traveling toward the poles will veer to the east because it will be ahead of, or faster than, the moving earth.

Hurricanes: A swirling powerful storm that is formed over a warm sea is called a hurricane. Hurricanes can cause significant amounts of damage to anything in its path through fierce winds, torrential rains, flooding, and its huge waves crashing ashore.

Hurricanes can kill more people and destroy more property than every other natural disaster. The calm central where the winds of the hurricane swirl around is called the eye. The eye is surrounded by a band of dark, tall clouds called the eye wall. The eye is serene as it is free of large clouds an rain. The eye is usually between 10 and 20 miles in diameter.

The strongest winds in the hurricane's eye wall are caused by the large changes in pressure.

Temperature: Temperature is very important in the development of hurricanes. First of all, in order for a hurricane to develop, waters must have a surface temperature greater than 80 degrees (26.5 degrees Celsius). This is the reason why hurricanes develop over tropical waters. August and September are the months where the water is the warmest, which is why they are the peak hurricane months.

Temperature is also the cause of rising and sinking air. (More about temperature in the link called atmospheric pressure.)

Wind Shear: Between higher and lower levels of the atmosphere, there must be little difference in wind shear. Wind shear is the speed and direction between winds at upper and lower levels of the air. Winds must remain stable (in unison) for the warm core of the storm to remain intact. If winds increased in speed or changed direction, the storm would probably disperse. Also, the bottom of the hurricane could go one way and the top could go another, and this could also cause a break up.

Atmospheric Pressure: Because of temperature, warm, moist air rises. This lowers the atmospheric pressure of the air beneath. Have you ever noticed while watching a weather forecast high and low pressures? Well, this rising of the air causes a low-pressure area.

In this area of low pressure, air between the surface of the water and the top of the atmosphere is less dense. Wind is created by the movement of air switching its placement between areas of high pressure and low pressure. Wind now is affected by the Coriolis Effect, which by now the hurricane can do some damage.

A hurricane viewed from space. 

Big storms in the atmosphere are usually centered on low-pressure areas and conform to those rules. Christophorus Buys Ballot in Holland first observed this in weather patterns in 1857, though William Ferrell in the US had predicted the phenomenon using arguments like the ones given here.

But don't expect to observe the effect in bathroom sinks. Water draining from a sink will usually swirl, because any rotation it has is greatly speeded up as it is drawn to the center of the sink. A slow circulation near the edges of the sink, e.g. because the sink itself is not completely symmetrical, becomes a fast vortex in the middle. The rotation of the Earth, however, is a much smaller factor than an uneven shape or heating of the sink, or a slow motion left from the time the sink was filled. If all 3 points A,B,C are inside the sink, with B at the drain, the difference in rotation speed (around the Earth's axis) between point B and either of the other two is typically only about 0.001 millimeter per second or about 1/7 of an inch per hour.

The scale of the motion is what makes the difference. Hurricanes obey the "law of Buys Ballot," but the swirling of water in sinks is primarily due to subtle asymmetries and "remembered motions" too slow for the eye to detect. Even tornadoes are not large enough--according to reports, they are equally likely to swirl in either direction.

Hurricane Andrew

On the scale of hurricanes and large mid-latitude storms, the Coriolis force causes the air to rotate around a low-pressure center in a cyclonic direction. Indeed, the term cyclonic not only means that the fluid (air or water) rotates in the same direction as the underlying Earth, but also that the rotation of the fluid is due to the rotation of the Earth. Thus, the air flowing around a hurricane spins counter-clockwise in the northern hemisphere, and clockwise in the southern hemisphere (as does the Earth, itself). In both hemispheres, this rotation is deemed cyclonic.

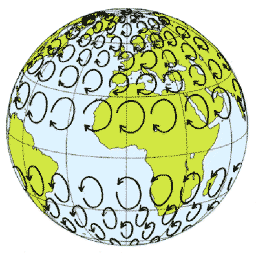
If the Earth did not rotate, the air would flow directly in towards the low-pressure center, but on a spinning Earth, the Coriolis force causes that air to be deviated with the result that it travels around the low-pressure center.

In the accompanying picture of the Caribbean, one can see the cyclonically spiraling clouds of Hurricane Andrew (at the mouth of the Mississippi) and of another vortex in the Atlantic. As you may already know, a hurricane just doesn't come out to be a hurricane. A hurricane must develop into a hurricane. The following paragraphs will explain how a hurricane comes about by using its stages.  Almost everything has to develop; they just do not "just come about." A hurricane is no different. So, let's take a look at the different hurricane stages.

First, there is the tropical disturbance. The tropical disturbance is an area of building rain clouds. These clouds are called cumulonimbus clouds, which usually rain for about 1 to 2 hours, but if conditions are right for a hurricane, more clouds will form.

Second comes the tropical depression, which is a low-pressure area that starts to blow in a pattern that is circular. This depression can be plotted on a weather map. This storm feeds other thunderstorms. Soon, the winds start blowing faster.

Next, the tropical storm. Meteorologists consider a tropical depression to be a tropical storm when the winds exceed 38 miles per hour. Clouds now have a well-defined circular shape, and usually the storm is still being fed from heat and water vapor from the sea.

Finally, we come to the development of a hurricane, which comes about when a tropical storm exceeds 74 miles per hour. Now the storm has a well-developed eye.

The Coriolis Force is very small indeed but affects the draining of a sink.

Water draining in the supposedly wrong way.

Compared to the rotations that one usually sees (tires on a traveling automobile, a compact disc playing music, or a draining sink) the rotation of the Earth is very small: only one rotation per day. The water in a sink might make a rotation in a few seconds and so have a rotation rate ten thousand times higher than that of the Earth. It should not be surprising, therefore, to learn that the Coriolis force is an order of magnitude smaller than any of the forces involved in these everyday-spinning things. The Coriolis force is so small, that it plays no role in determining the direction of rotation of a draining sink anymore than it does the direction of a spinning CD.

The direction of rotation of a draining sink is determined by the way it was filled, or by vortices introduced while washing. The magnitude of these rotations may be small, but they are nevertheless gargantuan by comparison to the rotation of the Earth. I decided to include a picture of a draining sink, and the first one I tried in my house was found to drain clockwise (the opposite of what the silly assertions would have it do here in the northern hemisphere). This direction was determined entirely by the way the tap filled the sink. The direction of rotation of a draining toilet is determined by the way the water just under the rim is squirted into the bowl when it is flushed.

Earth’s Rotation in a Draining Sink: Yes, but it is very difficult. Because the Coriolis force is so small, one must go to extraordinary lengths to detect it. But, it has been done. You cannot use an ordinary sink for it lacks the requisite circular symmetry: its oval shape and off-center drain render any results suspect. Those who have succeeded used a smooth pan of about one meter in diameter with a very small hole in the center.

A stopper (which could be removed from below so as to not introduce any spurious motion) blocked the hole while the pan was being filled with water. The water was then allowed to sit undisturbed for perhaps a week to let all of the motion die out, which was introduced during filling. Then, the stopper was removed (from below). Because the hole was very small, the pan drained slowly indeed. This was necessary, because it takes hours before the tiny Coriolis force could develop sufficient deviation in the draining water for it to produce a circular flow. With these procedures, it was found that the rotation was always cyclonic.

The formula for the Coriolis acceleration is:

F=

Where (here and below) v is the velocity in the rotating system, ω is the angular velocity (the rotation rate and orientation) of the rotating system. The equation may be multiplied by the mass of the relevant object to produce the Coriolis force.

Note that this is vector multiplication. In non-vector terms: At a given rate of rotation of the observer, the magnitude of the Coriolis acceleration of the object will be proportional to the velocity of the object and also to the sine of the angle between the direction of movement of the object and the axis of rotation.

The Coriolis effect is the behavior added by the Coriolis acceleration. The formula implies that the Coriolis acceleration is perpendicular both to the direction of the velocity of the moving mass and to the rotation axis.

So in particular:

If the velocity is zero, the Coriolis acceleration is zero.

If the velocity is parallel to the rotation axis, the Coriolis acceleration is zero.

If the velocity is straight (perpendicularly) inward to the axis, the acceleration will follow the direction of rotation.

If the velocity is following the rotation, the acceleration will be (perpendicularly) outward from the axis.

When considering atmospheric dynamics, the Coriolis acceleration (strictly a 3-d vector in the formula above) appears only in the horizontal equations due to the neglect of products of small quantities and other approximations. The term that appears is then

where k is a unit local vertical, f = 2ωsin(latitude) is called the Coriolis parameter and (u,v) are the horizontal components of the velocity.

Fictitious Force: The term “fictitious force” refers to a calculational tool in physics. In Newtonian mechanics, the basic laws of physics and equation of motion, F = ma only apply in an inertial frame of reference. It is sometimes useful or convenient to treat a problem in a reference frame which is non-inertial; in this case, the motion of the frame (rotation) manifests itself in a way that can be treated as a force within the context of the problem, now still using an equation of the form F = ma but where now the F includes these "fictitious" forces. The effect of these "fictitious" forces is perfectly real, but some terminology is necessary to distinguish these force terms that arise only from the noninertiality of the frame of reference from "real" forces, and thus they are usually, but not universally, called "fictitious."

The effect of a fictitious force is inferred to explain the accelerations observed in the non-inertial frame. Due to this, fictitious forces always act in direct proportion to the mass of the object they act on. The two most commonly-encountered fictitious forces are the Coriolis force and the centrifugal force, found in rotating frames of reference such as the surface of the Earth. While fictitious forces act mathematically identically to physical forces in the non-inertial frame, they are distinguishable from the others in that they do not appear to exist from the point of view of an inertial observer. Many times a non-inertial frame of reference is more useful than an inertial frame, so fictitious forces may be included to more easily describe the dynamics. For example, in a computer program describing the motion of a gas module in the atmosphere, terms for the Coriolis force are included along with true forces.

The concept of fictitious force is used in other models of mechanics as well. However, the precise mathematical definition of the term and classification of particular forces will be different in theories with different notions of forces and inertial reference frames. A true force in one theory of physics may act as a fictitious force in another theory that models similar phenomena in a different way. For example, in general relativity, freefalling observers are the ones who are in inertial frames of reference. This means that an observer standing on the surface of a planet is actually in an accelerated frame of reference, and that the gravity which that observer perceives is actually a fictitious force.

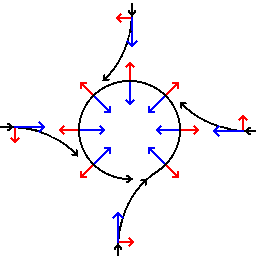
Schematic representation of flow around a low-pressure area in the Northern hemisphere. The pressure gradient force is represented by blue arrows, the Coriolis acceleration (always perpendicular to the velocity) by red arrows.

If a low pressure area forms in the atmosphere, air will tend to flow in towards it, but will be deflected perpendicular to its velocity by the Coriolis acceleration. A system of equilibrium can then establish itself creating circular movement, or a cyclonic flow.

The force balance is largely between the pressure gradient force acting towards the low-pressure area and the Coriolis acceleration acting away from the center of the low pressure. Instead of flowing down the gradient, the air tends to flow perpendicular to the air-pressure gradient and forms a cyclonic flow.

This is an example of a more general case of geostrophic flow in which air flows along isobars. On a non-rotating planet the air would flow along the straightest possible line, quickly leveling the air pressure. Note that the force balance is thus very different from the case of "inertial circles" (see below) which explains why mid-latitude cycles are larger by an order of magnitude than inertial circle flow would be.

This pattern of deflection, and the direction of movement is called Buys-Ballot’s Law. The pattern of flow is called a cyclone. A cyclone is the rotation of a volume of air about an area of low atmosphreric pressure. Cyclones are responsible for a wide variety of different metereological phenomena such as typhoons, hurricanes and tornadoes. Because of this, most weather forecasters avoid using the term cyclone without a qualifying term.

In the Northern Hemisphere the direction of movement around a low-pressure area is counterclockwise. In the Southern Hemisphere, the direction of movement is clockwise because the rotational dynamics is a mirror image there. Cyclones cannot form on the equator, and they rarely travel towards the equator because in the equatorial region the Coriolis parameter is small and exactly zero on the equator.

Draining Bathtubs/Toilets: People often ask whether the Coriolis effect determines the direction in which bathtubs or toilets drain, and whether water always drains in one direction in the Northern Hemisphere and in the other direction in the Southern Hemisphere. The answer is almost always no. The Coriolis effect is a few orders of magnitude smaller than other random influences on drain direction such as the geometry of the sink, toilet, or tub; whether it is flat or tilted, the direction in which water was initially added to it.

If one takes great care to create a flat circular pool of water with a small, smooth drain, to wait for eddies caused by filling it to die down, and to remove the drain from below (or otherwise remove it without introducing new eddies into the water) – then it is possible to observe the influence of the Coriolis effect in the direction of the resulting vortex. There is a good deal of misunderstanding on this point, as most people (including many scientists) do not realize how small the Coriolis effect is on small systems.¹

This is less of a puzzle once one remembers that the earth revolves once per day, but that a bathtub takes only minutes to drain. The increase in rotational speed around the plug hole is because water is being drawn towards the plughole, and so its radius of its mass to the point it is spinning around decreases so its rate of rotation increases from the low background level to a noticeable spin in order to conserve its angular momentum (the same effect as bringing your arms in on a swivel chair making it spin faster).

The time and space scales are important in determining the importance of the Coriolis effect. Weather systems are large enough to feel the curvature of the earth and generally rotate less than once a day so a similar timescale to the earth's rotation so the Coriolis effect is dominant. An unguided missile, if fired far enough, will travel far enough and be in the air long enough to notice the effect, but the dominant effect is the direction it was fired in. Long range shells landed close to, but to the right of where they were aimed until this was noted (or left if they were fired in the southern hemisphere, though most weren't). You don't worry about which hemisphere you're in when playing catch in the garden though this is exactly the same physics at a smaller scale. A bathtub is best approximated (in terms of scale) by a game of catch.

Coriolis Flow Meter: A practical application of the Coriolis effect is the mass flow meter, an instrument that measures the mass flow rate of a fluid through a tube. The operating principle was introduced in 1977 by Micro Motion Inc. Simple flow meters measure volume flow rate, which is proportional to mass flow rate only when the density of the fluid is constant. If the fluid has varying density, or contains bubbles, then the volume flow rate multiplied by the density is not an accurate measure of the mass flow rate. The Coriolis mass flow meter operating principle essentially involves rotation, though not through a full circle. It works by inducing a vibration of the tube through which the fluid passes, and subsequently monitoring and analysing the inertial effects that occur in response to the combination of the induced vibration and the mass flow.

Ballistics: In firing projectiles over a significant distance, the rotation of the Earth must be taken into account. During its flight, the projectile moves in a straight line (not counting gravitation and air resistance for now). The target, co-rotating with the Earth, is a moving target, so the gun must be aimed not directly at the target, but at a point where the projectile and the target will arrive simultaneously.

Molecular Physics: In polyatomic molecules, the molecule motion can be described by a rigid body rotation and internal vibration of atoms about their equilibrium position. As a result of the vibrations of the atoms, the atoms are in motion relative to the rotating coordinate system of the molecule. Coriolis effects will therefore be present and will cause the atoms to move in a direction perpendicular to the original oscillations. This leads to a mixing in molecular spectra between the rotational and vibrational levels.

Visualisation of the Coriolis Effect:

Above is a fluid assuming a parabolic shape as it is rotating. To demonstrate the Coriolis effect, a turntable can be used. If the turntable is flat, then the centrifugal force, which always acts outwards from the rotation axis, would lead to objects being forced out off the edge. If the turntable has a bowl shape, then the component of gravity tangential to the bowl surface will tend to counteract the centrifugal force. If the bowl is parabolic, and spun at the appropriate rate, then gravity exactly counteracts the centrifugal force and the only net force (bar friction, which can be minimised) acting is then the Coriolis force.

If the turntable is a dish with a rim and filled with liquid, then when the liquid is rotating it naturally assumes a parabolic shape (for the same reasons). If a liquid that sets after several hours is used, such as a synthetic resin, a permanent shape is obtained.

Disks cut from cylinders of dry ice can be used as pucks, moving around almost frictionlessly over the surface of the parabolic turntable, allowing dynamic phenomena to show themselves. To also get a view of the motions as seen from a rotating point of view, a video-camera is attached to the turntable in such a way that the camera is co-rotating with the turntable. This type of setup, with a parabolic turntable, at the center about a centimeter deeper than the rim is used at Massachusetts Institute of Technology (MIT) for teaching purposes. ²

Inertial Circles:

Schematic Representation. Inertial circles of air masses in the absence of other forces, calculated for a wind speed of approximately 50-70 m/s. If an object moves subject only to the Coriolis force, it will move in a circular trajectory called an 'inertial circle'.

In an inertial circle, the force balance is sometimes most easily understood as being between two fictitious forces, the centrifugal force (directed outwards) and the Coriolis force (directed inwards). The dynamics is thus quite different to mid-latitude cyclones or hurricanes, in which cases the force balance is between the pressure gradient force (directed inwards) and the Coriolis force (directed out).

In particular, this means that the direction of orbit is opposite to that of mid-latitude cyclones. The frequency of these oscillations is given by f, the coriolis parameter; and their radius by [1]: v / f, where v is the velocity of the air mass. On the Earth, a typical mid-latitude value for f is 10^-4; hence for a typical atmospheric speed of 10 m/s the radius is 100 km, with a period of about 14 hours. For a turntable rotating about once every 6 seconds, f is one, hence the radius of the circles, in cm, is numerically the same as the speed, in cm/s. The centrifugal force is v² / r and the Coriolis force vf, hence the forces balance when v² / r = vf, i.e. v / f = r, giving the expression above for the radius of the circles.

If the rotating system is a turntable, then f is constant and the trajectories are exact circles. On a rotating planet, f varies with latitude and the circles do not exactly close. Closer to the equator the component of the velocity towards or away from the Earth's axis is smaller. This component varies as sin(latitude), and this is taken into account in the parameter f. For a given velocity the oscillations are smallest at the poles as shown by the picture and would increase indefinitely at the equator, except the dynamics ceases to apply close to the equator. On a rotating planet the oscillations are only approximately circular, and do not form closed loops as indicated in the simplified picture.

Coriolis Effect Experiments: Next time you go to a playground, try this: Bring along a ball and a friend, and get on the merry-go-round. Try throwing the ball to your friend across the ride from you, or even just a few feet beside you, and see if they can catch it on the first attempt. They won't be able to, guaranteed. In fact, your throw will be way off. You'll feel your arm pulled strangely to one side as you make the throw, and once in flight, the ball will veer wildly. Physicists call this the "Coriolis effect," and it happens on any spinning platform.

Hurricanes swirl because of the Coriolis effect, the spinning platform being Earth itself. Contrary to popular belief, Coriolis forces do not control your bathroom drains--Earth doesn't spin that fast. But playing ball on a merry-go-round is definitely a Coriolis experience. Space travel could be a Coriolis experience, too.

Researchers have long known that spinning spaceships like a merry-go-round could solve a lot of problems: In weightlessness, astronaut's bones and muscles weaken. It's tricky to eat and drink, and even use the bathroom. Inside a spinning spaceship, on the other hand, there would be an artificial gravity (due to centrifugal forces) that keeps bodies strong and makes everyday living easier. The problem is, spinning spaceships also come with a strong Coriolis effect. Tossed objects veer. Reach out to touch a button ... and your finger lands in the wrong spot. Could astronauts adapt to this? And if so, could they adapt well enough to perform dependably in the life-threatening environment of space?

That's what researchers James Lackner and Paul DiZio are trying to figure out. With support from NASA's Office of Biological and Physical Research, these two scientists are performing a series of experiments with people in rotating chambers to learn how well astronauts might adjust to life onboard spinning spaceships. They also hope to find training techniques that could help ease the transition from non-spinning to spinning, and back again.

Above: An artist's concept of a spinning spaceship. Credit: John Frassanito & Associates, Inc.

"Experiments done in the 1960s seemed to show that people did not adapt well to rotation," says Lackner, the Meshulam and Judith Riklis, Professor of Physiology at Brandeis University in Waltham, Massachusetts. "But in those experiments, the subjects did not have well-defined goals for their movements. We have found that when a specific goal is given for the motion, people adapt rather quickly." Given specific motion goals (such as reaching out to touch a target), people in their study learned to move accurately after only 10 to 20 attempts. Such a rapid adjustment surprised the researchers.

Says DiZio, an associate professor of psychology at Brandeis, "we speculate that when a goal is present, the brain dictates the desired motion to the muscles more precisely. Deviations from that motion are detected more readily by sensory feedback to the brain."

Why should people have this natural ability to adapt to rotation?

Our bodies and brains might have evolved, to a degree, to deal with the Coriolis effect. Every time you turn and reach for something simultaneously, you have a brief Coriolis experience. Turning atop an office chair. Playing basketball. Spinning to see what made that strange noise behind you! In each case, your brain makes on-the-fly Coriolis adjustments.

Other discoveries surprised the researchers, too. For example, after rotating for a while, people in their study no longer perceived the Coriolis effect. The veering pull on their arms and legs seemed to vanish. Their brains had compensated for it, so their minds no longer took notice of it.

Even stranger, when test-subjects first return to a non-rotating environment, they report feeling a Coriolis-pull in the opposite direction. It's just a trick of the mind, notes DiZio. After another 10 to 20 attempts at a goal-oriented motion, their brains readjust to the non-rotating world, and the phantom effect goes away.

DiZio and Lackner have found that people can adapt to rotational speeds as fast as a carnival-ride-like 25 rpm. That is about as fast as people turn their bodies during day-to-day life. For comparison, a spinning spaceship would likely rotate more slowly, perhaps 10 rpm, depending on the size and design of the craft.

To exert more control over the conditions of their experiment, the researchers have tried something innovative: simulating the Coriolis effect with a robotic arm. Seated subjects would try to make certain motions with their arm while the robotic arm gently pulls on their wrist in a way that mimics the Coriolis effect.

The advantage of this approach is that the robotic arm can be reprogrammed to pull in a variety of ways, thus testing how subjects respond to different conditions. Using the arm, DiZio and Lackner have discovered that people can adapt to a small, variable force even when it's masked by a larger, constant force. So, for example, astronauts should be able to adapt to a variable Coriolis effect in spite of some constant background force, such as the steady push of a spacecraft's ion-propulsion thrusters.

Many questions remain un-answered. Do results based on arm motions apply to the whole body? Does carrying heavy tools make a difference? After adapting once, can a person re-adapt more easily later? What's the best way to train astronauts for life in a rotating home?

Coriolis Effect Affects Wind Direction: Air flows from areas of higher pressure to areas of lower pressure. Based on this fact, the predicted wind direction for the area on the left side of this satellite image would be from the southeast. The Coriolis effect influences wind by deflecting its path to the right in the Northern Hemisphere. The sequence of weather satellite images shows that the actual wind direction is from the southwest. The satellite images show atmospheric motion over the northern Pacific Ocean for a 36-hour period.

The Coriolis effect on the wind:

4/'98

A further explanation of the Coriolis effect (Section 11.4) is provided by Fig 1. The left part (a) shows a westerly wind blowing over Australia. Part (b) shows the wind blowing in the same direction (as seen in a fixed frame of reference) three hours later, when the Earth’s rotation has turned the continent around by 45 degrees. Now this identical wind appears to come from the southwest. In other words, the origin of the wind and its destination seem to have turned anticlockwise (i.e.?widdershins?) as though pushed to the left. This apparent leftwards torsion on the wind in the southern hemisphere is what we mean by the Coriolis effect. (It is rightwards in the northern hemisphere.) In reality the Coriolis force is largely balanced by the pressure gradient force, so that the wind direction typically changes little relative to the Earth over the course of 3 hours. This balanced wind is known as the geotropic wind.

Fig. 1. Australia as seen from outer space at (a) time 0 and (b) time 0+3h.

Fig 2. Illustration of how an object on a straight path (from an outsider's perspective) is seen, by an observer on the clockwise-rotating platform, to rotate in a counterclockwise direction. In other words, from a 'southern hemisphere' perspective, the object is 'pulled' to the left.

Another hand waving attempt to explain the Coriolis force is given in Fig 2. The left diagram (a) shows an object flying along a straight path across a rotating platform, which can be thought of as the Earth with the South Pole in the center. M maintaining the analogy with the Earth, we assume that it takes about 12 hours to travel from left to right across the diagram. At various times (numbered 1 thru 20 on the diagram), an observer on the Earth sees this object in the directions shown in (a) and transposed to a common origin in (b). From the perspective of the observer on Earth, the freely moving object appears to be pulled to the left.

Yet another way of persuading people of the reality of the Coriolis effect was described by Durran and Domonkos (1). It involves a frictionless puck moving over a rotating parabolic dish, and two video cameras. The puck consisted of a 1.2-cm disk of dry ice, which automatically slides on a layer of carbon-dioxide gas.

The Coriolis Force on Astronauts: Wheel-shaped space station with visiting winged spaceship.

(Von Braun's, from the early 1950's)

The science-fiction film "2001: A Space Odyssey" featured spinning space station, whose rotation provided the crew with "artificial gravity." It was a wheel-shaped structure, with hollow spokes connecting the wheel to a cabin in the center (drawing). The cabin in the middle was where transfers between the station and visiting spacecraft took place. Given such a rotation, something like gravity would indeed be produced, with "down" being towards the outside (Larry Niven expanded that notion into the fanciful science-fiction novel "Ringworld" and its sequels). When calculating this effect it is simplest to use the station's frame of reference and add a centrifugal force to all other forces there.

However, when one moves in this rotating environment, especially motion up and down the spokes, an additional force is encountered. Imagine an astronaut moving along one of the spokes, say from point A in the drawing to point B--most likely, climbing a ladder, since such motion goes against the station's "artificial gravity." At any point, as viewed in the frame of the outside world, the astronaut is also rotating around the station's axis.

At both point A and B, the rotation is in the same direction, but at B it is slower, because that point is nearer to the axis of rotation and therefore describes a smaller circle.

What happens at B to the extra speed the astronaut had at A? According to Newton's first law, loosely applied, the astronaut would tend to keep that extra speed and would therefore be pushed against the side of the spoke (direction of the arrows). That push is the Coriolis force. When the motion is in the opposite direction, from B to A, the direction of the force is reversed.

Could animals be using some “factor X” sensory capability not yet recognized?

Answers by Melvin Kreithen: “If we are going to understand animal navigation, we must discover a new sensory channel. Existing ones are not sufficient to explain the behavior.” In 1942 Henry L. Yeagley, a Pennsylvania State College physicist, proposed that a homing pigeon could tune into the earth’s magnetic field and, simultaneously, sense the effect of the earth’s rotation on its flight path—the Coriolis effect, named after the French engineer who described it.

Yeagley argued that magnetic and Coriolis information would create a “navigational grid work” akin to lines of latitude and longitude, thus supplying the two coordinates for position finding. Those who thought it farfetched that a pigeon could sense the earth’s rotation dismissed Yeagley’s experiments. “Though Yeagley didn't really prove his case, history is showing that he was asking the right questions,” says Kreithen, who agrees that a pigeon might sense the earth's rotation. “People on a revolving disk detect rotations as slow as one every 2.4 hours. That's just an order of magnitude away from detecting the rotation of the earth. So it's not unreasonable to ask if an animal has that ability.” James Gould comments: “Given the contradictory results we get in pigeon studies, we probably should go out and do Yeagley’s experiments again. “At the turn of the century,” Gould continues, “we assumed that animals were color-blind, and it was an incredible shock for some of us to learn that bees had color vision. Later on we discovered that fish could hear, pigeons could see ultraviolet light, and snakes have an infrared sensing apparatus. “The whole history of animal behavior is the animals taking us by surprise,” says Gould. “Why shouldn't they have some surprises for us now?” Source: National Geographic, June 1991.

Contributors to Coriolis Effect Research

Coriolis Force: Gaspard-Gustave de Coriolis (May 21, 1792-September 19, 1843), mathematicians, mechanical engineer, and scientist born in Paris, France. In 1816 Coriolis became a tutor at the Ecole Polytechnique. Here he carried out experiments on friction and hydraulics. In 1829 Coriolis published a textbook, Calcul de l'Effet des Machines (Calculation of the Effect of Machines) which presented mechanics in a way that could be readily be applied by industry. In this period the correct expression for kinetic energey, , and its relation to mechanical work became established.

During the following years Coriolis worked to extend the notion of kinetic energy and work to rotating systems. The first of his papers, Sur le principe des forces vives dans les mouvements relatifs des machines (on the principle of kinetic energy in the relative motion in machines) was read to the Académie des Sciences (Coriolis 1832). Three years later came the paper that would make his name famous, Sur les équations du mouvement relatif des systèmes de corps (on the equations of relative motion of a system of bodies (Coriolis 1835). Coriolis's papers do not deal with the atmosphere or even the rotation of the earth, but with the transfer of energy in rotating systems like waterwheels.

Coriolis's name began to appear in the meteorological literature at the end of the nineteenth century, although the term “Coriolis force” was not used until the beginning of the twentieth century. Today, the name Coriolis has become strongly associated with meteorology, but all major discoveries about the general circulation and the relation between the pressure and wind fields were made without knowledge about Gaspard Gustave Coriolis. Coriolis died at the age of 51 in Paris.

Christophorus Henricus Diedericus Buys Ballot: (October 10 1817-February 3, 1890) He was a Dutch Chemist and metereologist after whom Buy’s Ballot Law and the Buys Ballot table are called. The son of a Dutch Reformed minister, Buy Ballot attended the Gymnasium at Zaltbommel and the Hogenshool University of Utrecht. After receiving his doctorate in 1844, he became lecturer in mineralogy and geology at Utrecht; he added theoretical chemistry in 1846. In 1847 he was appointed professor of mathematics and from 1867 until his retirement he was professor of physics.

Buys Ballot is best known for his accomplishments in the field of mwtereology, specifically the explanation of the direction of air flow in large weather systems. Furthermore, he founded the Royal Dutch Meteorological Institute (KNMI)) in 1854, and he remained its chief director until his death. He was one of the first to see the need for international cooperation, and in 1873 became the first chairman of the International Meteorological Committee, a precursor of the World Metereological Organmization (WMO).

Buys Ballot Law states, “That if a person in the Northern Hemisphere stands with his back to the wind, the low atmospheric pressure is found to his left.” His main research effort in meteorology went into examining long time series for regularities; he was more concerned with establishing the regularities than in explaining them. He made no contributions to the theory of meteorology which is perhaps surprising given his training in physics. The contrast with his American contemporary and slightly earlier discoverer of Buy-Ballot's law William Ferrel is striking.

Buys Ballot devised a tabular method for investigating periodicity in time series. In 1847 he used the table now named after him to determine the period of the sun's rotation from daily observations of temperature in the Netherlands from 1729 to1846.

Time Series Investigation by Buys Ballot: In statisticss and signal processing, a time series is a sequence of data points, measured typically at successive times, spaced apart at uniform time intervals. Time series analysis comprises methods that attempt to understand such time series, often either to understand the underlying theory of the data points (where did they come from? what generated them?) or to make forecasts (predictions). Time series prediction is the use of a model to predict future events based on known past events: to predict future data points before they are measured. The standard example is the opening price of a share of stock based on its past performance.

Models for time series data can have many forms. Two broad classes of practical importance are the moving average (MA) models, and the autoregressive (AR) models. These two classes depend linearly on previous data points and are treated in more detail in the article on autoregressive moving averaging models (ARMA). Non-linear dependence on previous data points is of interest because of the possibility of producing a cahotic time series.

A number of different notations are in use for time-series analysis

is a common notation which specifies a time series X which is indexed by the natural numbers.

Tools for investigating time-series data include: Consideration of the autocorrelation function and spectral density function; Performionga Fourier transform to investigate the series in the frequency domain; the use of a filter to remove unwanted noise; artifical neural networks; time frequency analysis techniques; and chaotic analysis.

Chaos Theory: Chaos theory deals with the behavior of certain nonlinear dynamcycal systems that (under certain conditions) exhibit the phenomenon known as chaos, most famously characterised by sensitivity to initial conditions (butterfly effect). As a result of this sensitivity, the observed behavior of physical systems that exhibit chaos appears to be random, even though the model of the system is 'deterministic' in the sense that it is well defined and contains no random parameters.

Examples of such systems include the atmosphere, solar system, plate tectonics, turbulent fluids, economies, and population growth.

A plot of the trajectory Lorenz system for values r=28, σ = 10, b = 8/3.

Systems that exhibit mathematical chaos are deterministic and thus orderly in some sense; this technical use of the word chaos is at odds with common parlance, which suggests complete disorder. When we say that chaos theory studies deterministic systems, it is necessary to mention a related field of physics called quantum chaos theory that studies non-deterministic systems following the laws of quantum mechanics.

William Ferrel (1817-1801), an American metereologist, developed theories which explained the mid-latitude atmospheric calculation cell in detail, and it is after him that the Ferrel cell is named. Ferrel demonstrated that it is the tendency of rising warm air, as it rotates under the effect of the Coriolis force, to pull in air from more southerly, warmer regions and transport it poleward. It is this rotation which creates the complex curvatures in the frontal systems separating the cooler Arctic air to the north from the warmer continental tropical air to the south.

William Ferrel

Ferrel’s Law: Ferrel's law, named after William Ferrel (1717-1891), is a natural law in physical geography and metreology. “If a body moves in any direction on the earths surface, there is a deflecting force arising from the earths rotation, which deflects it to the right in the norhtern hemisphere and to the left in the southern hemisphere.” This law applies to every body that is set in motion upon the surface of the rotating earth, but usually the duration of the motion of any body due to a single impulse is so brief, and there are so many frictional disturbances, that it is not easy to observe the results of this deflecting force. The movements of the atmosphere, however, are upon a scale large enough to make this observation easy, and the simplest evidence is obtained from a study of the direction of the air movements in the great wind systems of the globe.

Atmospheric circulation is the large-scale movement of air, and the means (together with the ocean circulation) which is smaller by which heat is distributed on the surface of the Earth. The large-scale structure of the atmospheric circulation varies from year to year but the basic structure remains fairly constant. However, individual weather systems - midlatitude depressions, or tropical convective cells - occur "randomly," and it is accepted that weather cannot be predicted beyond a fairly short limit: perhaps a month in theory, or (currently) about ten days in practice). Nonetheless the average of these systems - the climate - is quite stable

The Ferrel cell is usually shown between the Hadley and Polar cells, e.g. atmospheric circulation. It is named after William Ferrel, who was concerned with describing the surface flow in the temperate zone of air that came from the Horse Latitudes, namely the Westerlies. In the region of the Atlantic ocean the Westerlies are the northern part of the general circulation of air about the high pressure system that sits over the Horse latitudes. The main 'problem' with the Ferrel cell is that it is thermally indirect. However, the true atmospheric circulation is rather more complex than the simplified zonal mean pictures would lead one to suspect. It is possible to argue that the Ferrel cell does not exist.

Bibliography:

Buys-Ballot's law, C.H.D. Buys Ballot, Web site: http://www.brainyencyclopedia.com/encyclopedia/c/c_/c_h_d__buys_ballot.html

300 kb Quicktime movie of the Mars-bound ship in motion. Credit: John Frassanito & Associates, Inc.Web site:

Buys Ballot, Christoph Hendrik Diederik, Microsoft ® Encarta ® Reference Library 2004. © 1993-2003 Microsoft Corporation. All rights reserved.

Gaspard-Gustave de Coriolis Web site: http://www.brainyencyclopedia.com/encyclopedia/g/ga/gaspard_gustave_coriolis.html

Gaspard-Gustave de Coriolis Web site: http://en.wikipedia.org/wiki/Gaspard-Gustave_de_Coriolis

Cyclone Theory, Web site: http://en.wikipedia.org/wiki/Cyclone

C.H.D. Buys Ballot, Wikipedia Encyclopedia, Web site: http://en.wikipedia.org/wiki/Cyclone

William Ferrel, Ferrel Law, Web site: http://en.wikipedia.org/wiki/Ferrel%27s_law

Could animals be using some “factor X” sensory capability not yet recognized?

by Melvin Kreithen, Microsoft ® Encarta ® Reference Library 2004. © 1993-2003 Microsoft Corporation. All rights reserved.

Solar Navigatinm by Birds, Microsoft ® Encarta ® Reference Library 2004. © 1993-2003 Microsoft Corporation. All rights reserved.

Coriolis force, Microsoft ® Encarta ® Reference Library 2004. © 1993-2003 Microsoft Corporation. All rights reserved.

Tropical Storms,Microsoft ® Encarta ® Reference Library 2004. © 1993-2003 Microsoft Corporation. All rights reserved.

Trade Winds, Microsoft ® Encarta ® Reference Library 2004. © 1993-2003 Microsoft Corporation. All rights reserved.

Giant Ocean cataracts, Microsoft ® Encarta ® Reference Library 2004. © 1993-2003 Microsoft Corporation. All rights reserved.

Meteorology, Microsoft ® Encarta ® Reference Library 2004. © 1993-2003 Microsoft Corporation. All rights reserved.

Gaspaer de Coriolis, Microsoft ® Encarta ® Reference Library 2004. © 1993-2003 Microsoft Corporation. All rights reserved.

Coriolis Force and Noninertial Effects, David H. McIntyre, Department of Physics, Oregon State University, Web Site: http://www.physics.orst.edu/~mcintyre/coriolis/

Physical Effects of the Earth's Rotation (Coriolis Effects), Web Site: cseligman.com/text/planets/coriolis.htm

Centripedal force,Web Site: hyperphysics.phy-astr.gsu.edu/hbase/corf.html

Coriolis Force and Noninertial Effects, David H. McIntyre, Department of Physics, Oregon State University, Web Site: http://www.physics.orst.edu/~mcintyre/coriolis/

Dr. James Hayes White Paper, Subject: Coriolis Effects on Strategic Weapon Systems, Colsa Corporation, December 2005.