February 28, 2005
History
topic: Overview of Chinese Mathematics
By
Dr. Frank J. Collazo
Several
factors led to the development of mathematics in China being, for a long
period, independent of developments in other civilisations. The geographical
nature of the country meant that there were natural boundaries (mountains and
seas) which isolated it. On the other hand, when the country was conquered by
foreign invaders, they were assimilated into the Chinese culture rather than
changing the culture to their own. As a consequence there was a continuous
cultural development in China from around 1000 BC and it is fascinating to
trace mathematical development within that culture. There are periods of rapid
advance, periods when a certain level was maintained, and periods of decline.
The
first thing to understand about ancient Chinese mathematics is the way in which
it differs from Greek mathematics. Unlike Greek mathematics there is no
axiomatic development of mathematics. The Chinese concept of mathematical proof
is radically different from that of the Greeks, yet one must not in any sense
think less of it because of this. Rather one must marvel at the Chinese
approach to mathematics and the results to which it led.
Chinese
mathematics was, like their language, very concise. It was very much problem
based, motivated by problems of the calendar, trade, land measurement,
architecture, government records and taxes. By the fourth century BC counting
boards were used for calculating, which effectively meant that a decimal place
valued number system was in use. It is worth noting that counting boards are
uniquely Chinese, and do not appear to have been used by any other
civilisation.
Our
knowledge of Chinese mathematics before 100 BC is very sketchy although in 1984
the Suan shu shu (A Book on Arithmetic) dating from around 180 BC was
discovered. It is a book written on bamboo strips and was found near Jiangling
in Hubei province. The next important books of which we have records are a
sixteen chapter work Suanshu (Computational prescriptions) written by Du
Zhong and a twenty-six chapter work Xu Shang suanshu (Computational
prescriptions of Xu Shang) written by Xu Shang. Neither of these texts has
survived and little is known of their content. The oldest complete surviving
text is the Zhoubi suanjing (Zhou Shadow Gauge Manual) which was
compiled between 100 BC and 100 AD (see the article on The Ten Classics). It is
an astronomy text, showing how to measure the positions of the heavenly bodies
using shadow gauges which are also called gnomons, but it contains important
sections on mathematics. It gives a clear statement on the nature of Chinese
mathematics in this period (see for example [2]:-
The
method of calculation is very simple to explain but has wide application. This
is because a person gains knowledge by analogy, that is, after understanding a
particular line of argument they can infer various kinds of similar reasoning
... Whoever can draw inferences about other cases from one instance can
generalise ... really knows how to calculate... . To be able to deduce and then
generalise.. is the mark of an intelligent person.
The
Zhoubi suanjing contains a statement of the Gougu rule (the Chinese
version of Pythagoras's theorem) and applies it to surveying, astronomy, and other
topics. Although it is widely accepted that the work also contains a proof of
Pythagoras's theorem, Cullen in [39] disputes this, claiming that the belief is
based on a flawed translation given by Needham in [13].
In
fact much Chinese mathematics from this period was produced because of the need
to make calculations for constructing the calendar and predicting positions of
the heavenly bodies. The Chinese word 'chouren' refers to both mathematicians
and astronomers showing the close link between the two areas. One early
'choren' was Luoxia Hong (about 130 BC - about 70 BC) who produced a calendar
which was based on a cycle of 19 years.
The
most famous Chinese mathematics book of all time is the Jiuzhang suanshu
or, as it is more commonly called, the Nine Chapters on the Mathematical Art.
The book certainly contains contributions to mathematics which had been made
over quite a long period, but there is little in the original text to
distinguish the precise period of each. This important work, which came to
dominate mathematical development and style for 1500 years, is discussed in the
article Nine Chapters on the Mathematical Art. Many later developments came
through commentaries on this text, one of the first being by Xu Yue (about 160
- about 227) although this one has been lost.
A
significant mathematical advance was made by Liu Hui (about 220 - about 280)
who wrote his commentary on the Jiuzhang suanshu or Nine Chapters on the
Mathematical Art in about 263. Dong and Yao write [24]:-
Liu
Hui, a great mathematician in the Wei Jin Dynasty, ushered in an era of
mathematical theorisation in ancient China, and made great contributions to the
domain of mathematics. From the "Jiu Zhang Suan Shu Zhu" and the
"Hai Dao Suan Jing" it can be seen that Liu Hui made skilful use of
thinking in images as well as in logical and dialectical ways. He solved many
mathematical problems, pushing his mathematical reasoning further along the
dialectical way.
Liu
Hui gave a more mathematical approach than earlier Chinese texts, providing
principles on which his calculations are based. He found approximations to
using regular polygons with 3 ![]() 2n
sides inscribed in a circle. His best approximation of was 3.14159 which he
achieved from a regular polygon of 3072 sides. It is clear that he understood
iterative processes and the notion of a limit. Liu also wrote Haidao
suanjing or Sea Island Mathematical Manual (see the article on The
Ten Classics) which was originally an appendix to his commentary on Chapter 9
of the Nine Chapters on the Mathematical Art. In it Liu uses Pythagoras's
theorem to calculate heights of objects and distances to objects which cannot
be measured directly. This was to become one of the themes of Chinese
mathematics.
2n
sides inscribed in a circle. His best approximation of was 3.14159 which he
achieved from a regular polygon of 3072 sides. It is clear that he understood
iterative processes and the notion of a limit. Liu also wrote Haidao
suanjing or Sea Island Mathematical Manual (see the article on The
Ten Classics) which was originally an appendix to his commentary on Chapter 9
of the Nine Chapters on the Mathematical Art. In it Liu uses Pythagoras's
theorem to calculate heights of objects and distances to objects which cannot
be measured directly. This was to become one of the themes of Chinese
mathematics.
About
fifty years after Liu's remarkable contributions, a major advance was made in
astronomy when Yu Xi discovered the precession of the equinoxes. In mathematics
it was some time before mathematics progressed beyond the depth achieved by Liu
Hui. For example Sun Zi (about 400 - about 460) wrote his mathematical manual
the Sunzi suanjing which on the whole provides little new. However, it
does contains a problem solved using the Chinese remainder theorem, being the
earliest known occurrence of this type of problem.
This
text by Sun Zi was the first of a number of texts over the following two
hundred years which made a number of important contributions. Xiahou Yang
(about 400 - about 470) was the supposed author of the Xiahou Yang suanjing
(Xiahou Yang's Mathematical Manual) which contains representations of numbers
in the decimal notation using positive and negative powers of ten. Zhang
Qiujian (about 430 - about 490) wrote his mathematical text Zhang Qiujian
suanjing (Zhang Qiujian's Mathematical Manual) some time between 468 and
486. Its 92 problems illustrate the formula for summing an arithmetic
progression. Perhaps it is most famous for presenting the 'Hundred fowls
problem' which is an indeterminate problem with three non-trivial solutions.
One
of the most significant advances was by Zu Chongzhi (429-501) and his son Zu
Geng (about 450 - about 520). Zu Chongzhi was an astronomer who made accurate
observations which he used to produce a new calendar, the Tam-ing Calendar
(Calendar of Great Brightness), which was based on a cycle of 391 years. He
wrote the Zhui shu (Method of Interpolation) in which he proved that
3.1415926 < p < 3.1415927. He recommended using 355/113
as a good approximation and 22/7 in less accurate work.
With his son Zu Geng he computed the formula for the volume of a sphere using
Cavalieri's principle (see [25]). The beginnings of Chinese algebra is seen in
the work of Wang Xiaotong (about 580 - about 640). He wrote the Jigu
suanjing (Continuation of Ancient Mathematics), a text with only 20
problems which later became one of the Ten Classics. He solved cubic equations
by extending an algorithm for finding cube roots. His work is seen as a first
step towards the "tian yuan" or "coefficient array method"
or "method of the celestial unknown" of Li Zhi for computing with
polynomials.
Interpolation
was an important tool in astronomy and Liu Zhuo (544-610) was an astronomer who
introduced quadratic interpolation with a second order difference method.
Certainly Chinese astronomy was not totally independent of developments taking
place in the subject in India and similarly mathematics was influenced to some
extent by Indian mathematical works, some of which were translated into Chinese.
Historians argue today about the extent of the influence on the Chinese
development of Indian, Arabic and Islamic mathematics. It is fair to say that
their influence was less than it might have been, for the Chinese seemed to
have little desire to embrace other approaches to mathematics. Early
trigonometry was described in some of the Indian texts which were translated
and there was also development of trigonometry in China. For example Yi Xing
(683-727) produced a tangent table.
From
the sixth century mathematics was taught as part of the course for the civil
service examinations. Li Chunfeng (602 - 670) was appointed as the
editor-in-chief for a collection of mathematical treatises to be used for such
a course, many of which we have mentioned above. The collection is now called
The Ten Classics, a name given to them in 1084.
The
period from the tenth to the twelfth centuries is one where few advances were
made and no mathematical texts from this period survive. However Jia Xian
(about 1010 - about 1070) made good contributions which are only known through
the texts of Yang Hui since his own writings are lost. He improved methods for
finding square and cube roots, and extended the method to the numerical
solution of polynomial equations computing powers of sums using binomial
coefficients constructed with Pascal's triangle. Although Shen Kua (1031 -
1095) made relatively few contributions to mathematics, he did produce
remarkable work in many areas and is regarded by many as the first scientist.
He wrote the Meng ch'i pi t'an (Brush talks from Dream Brook) which
contains many accurate scientific observations.
The
next major mathematical advance was by Qin Jiushao (1202 - 1261) who wrote his
famous mathematical treatise Shushu Jiuzhang (Mathematical Treatise in
Nine Sections) which appeared in 1247. He was the first of the great thirteenth
century Chinese mathematicians. This was a period of major progress during
which mathematics reached new heights. The treatise contains remarkable work on
the Chinese remainder theorem, gives an equation whose coefficients are
variables and, among other results, Heron's formula for the area of a triangle.
Equations up to degree ten are solved using the Ruffini-Horner method.
Li
Zhi (also called Li Yeh) (1192-1279) was the next of the great thirteenth
century Chinese mathematicians. His most famous work is the Ce yuan hai jing
(Sea mirror of circle measurements). written in 1248. It contains the
"tian yuan" or "coefficient array method" or "method
of the celestial unknown" which was a method to work with polynomial
equations. He also wrote Yi gu yan duan (New steps in computation) in
1259 which is a more elementary work containing geometric problems solved by
algebra. The next major figure from this golden age of Chinese mathematics was
Yang Hui (about 1238 - about 1298). He wrote the Xiangjie jiuzhang suanfa
(Detailed analysis of the mathematical rules in the Nine Chapters and their
reclassifications) in 1261, and his other works were collected into the Yang
Hui suanfa (Yang Hui's methods of computation) which appeared in 1275. He
described multiplication, division, root-extraction, quadratic and simultaneous
equations, series, computations of areas of a rectangle, a trapezium, a circle,
and other figures. He also gave a wonderful account of magic squares and magic
circles.
Guo
Shoujing (1231-1316), although not usually included among the major
mathematicians of the thirteen century, nevertheless made important
contributions. He produced the Shou shi li (Works and Days Calendar),
worked on spherical trigonometry, and solved equations using the Ruffini-Horner
numerical method. He also developed a cubic interpolation formula tabulating
differences of the accumulated difference as in Newton's forward difference
interpolation method.
The
last of the mathematicians from this golden age was Zhu Shijie (about 1260 -
about 1320) who wrote the Suanxue qimeng (Introduction to mathematical
studies) published in 1299, and the Siyuan yujian (True reflections of
the four unknowns) published in 1303. He used an extension of the
"coefficient array method" or "method of the celestial
unknown" to handle polynomials with up to four unknowns. He also gave many
results on sums of series. This represents a high point in ancient Chinese
mathematics.
The
decline in Chinese mathematics from the fourteenth century was not by any means
dramatic. The Nine Chapters on the Mathematical Art continued to be the model
for mathematical learning and new works based in it continued to appear. For
example Ding Ju published the Ding ju suan fa (Ding Ju's arithmetical
methods) in 1355, He Pingzi published the Xiangming suan fa
(Explanations of arithmetic) in 1373, Liu Shilong published the Jiu zhang
tong ming suanfa (Methods of calculation in the 'Nine Chapters') in 1424,
and Wu Jing published the Jiu zhang suan fa bi lei da quan (Complete
description of the 'Nine Chapters') in 1450. Wu Jing was an administrator in
the province of Zhejing and his arithmetical encyclopaedia contained all the
246 problems of the Nine Chapters. Again Cheng Dawei (1533 - 1606) published
the Suanfa tong zong (General source of computational methods) in 1592
which is written in the style of the Nine Chapters on the Mathematical Art but
provides an even larger collection of 595 problems.
The
books we have just listed show mathematical activity, but they did not take
forward the methods of polynomial algebra. On the contrary, the deep works of
the 13th century ceased to be even understood much less developed
further. Xu Guangqi (1562 - 1633) certainly recognised exactly this and offered
possible explanations including scholars neglecting practical computational
tools and an identification of mathematics with mystical numerology under the
Ming dynasty. Other factors must be that the books describing the advanced
methods were, in the Chinese tradition, very terse, and without teachers to
pass on an understanding it became increasingly difficult for scholars to learn
directly from the texts. Xu Guangqi was the first native of China to publish translations
of European books in Chinese. Collaborating with Matteo Ricci he translated
Western books on mathematics, hydraulics, and geography. Certainly this does
not mark the end of the Chinese mathematics tradition, but from the time of
Matteo Ricci and other Western missionaries China was greatly influenced by
other mathematical traditions.
It
is impossible in an article of this length to mention many of the numerous
contributions from this period on. Let us mention one important family,
however, namely the Mei family. The most famous member of this family was Mei
Wending (1633-1721) and his comment on the golden section is typical of the
sensible attitude he took towards Western mathematics (see for example [9]):-
After
having understood how to make use of the golden section, I began to believe
that the different geometrical methods could be understood and that neither the
missionaries attitude of considering this simple technique as a divine gift,
nor the Chinese attitude of rejecting it as heresy is correct.
Mei
chose not to take a government post as most mathematicians did, but rather
decided to devote himself to mathematics and its teaching. He travelled widely
throughout China and gained great fame leading to many people becoming his
pupils. Two of his brothers, Mei Wenmi and Mei Wennai, worked on astronomy and
mathematics. Mei Wending was assisted later in his life by his son Mei Yiyan.
Mei Juecheng (1681-1763), who was Mei Wending's grandson, was asked in 1705 by
Emperor Kangxi to be editor-in-chief of the major mathematical encyclopaedia Shuli
jingyun (Collected basic principles of mathematics) (1723). Mei Juecheng
also edited his grandfather Mei Wending's work producing the Meishi congshu
jiyao (Collected works of the Mei family) in 1761.
Certain
people from the eighteenth century onwards did an excellent job in recording
the Chinese tradition so that much of it is still accessible to us today. For
example Dai Zhen (1724 - 1777) became an editor for the Siku quanshu
(Complete library of the four branches of literature) which was a project set
up by Emperor Qianlong in 1773. He edited a new edition of the Nine Chapters on
the Mathematical Art after copying the complete text as part of this project.
Ruan Yuan (1764 - 1849) produced his famous work the Chouren zhuan or Biographies
of astronomers and mathematicians containing biographies of 275 Chinese and
41 Western "mathematicians". Many biographical details of Chinese
mathematicians recorded in this Archive are known through this work. Li Rui
(1768 - 1817) assisted Ruan Yuan. He was a highly productive mathematician who
died when at the height of his abilities. His most important work is Lishi
suan xue yi shu (Collected mathematical works of Li Rui).
It
is to the credit of Chinese mathematicians that they did not let their
mathematical tradition be replaced by the western tradition. For example Li
Shanlan (1811-1882) is important as a translator of Western science texts but
he is most famous for his own mathematical contributions. He produced his own
versions of logarithms, infinite series, and combinatorics which did not follow
the style of western mathematics but his research naturally developed out of
the foundations of Chinese mathematics. There were many other efforts to
promote Chinese mathematics, and in particular a mathematics journal, the Suanxue
bao, was set up in 1899. The editors wrote:-
Western
methods should not be adulated and Chinese methods despised.
Western
mathematicians began lecturing in China during the early years of the twentieth
century. For example Knopp taught there between 1910 and 1917, and Turnbull
between 1911 and 1915. Chinese students began to study mathematics abroad and
in 1917 Minfu Tah Hu obtained a doctorate from Harvard. China was represented
for the first time at the International Congress of Mathematicians in Zürich in
1932. The Chinese mathematical Society was formed in 1935.
Article
by: J J O'Connor
and E F Robertson
December 2003
MacTutor
History of Mathematics
[http://www-history.mcs.st-andrews.ac.uk/HistTopics/Chinese_overview.html]
History topic: Chinese
numerals
In
1899 a major discovery was made at the archaeological site at the village of
Xiao dun in the An-yang district of Henan province. Thousands of bones and
tortoise shells were discovered there which had been inscribed with ancient
Chinese characters. The site had been the capital of the kings of the Late
Shang dynasty (this Late Shang is also called the Yin) from the 14th
century BC. The last twelve of the Shang kings ruled here until about 1045 BC
and the bones and tortoise shells discovered there had been used as part of
religious ceremonies. Questions were inscribed on one side of a tortoise shell,
the other side of the shell was then subjected to the heat of a fire, and the
cracks which appeared were interpreted as the answers to the questions coming
from ancient ancestors.
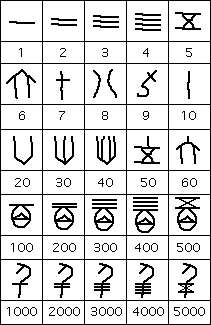
The importance of these finds, as far as learning about the ancient Chinese
number system, was that many of the inscriptions contained numerical
information about men lost in battle, prisoners taken in battle, the number of
sacrifices made, the number of animals killed on hunts, the number of days or
months, etc. The number system which was used to express this numerical
information was based on the decimal system and was both additive and
multiplicative in nature. Here is a selection of the symbols that were used.
By having multiplicative properties we mean that 200 is represented by the
symbol for 2 and the symbol for 100, 300 is represented by the symbol for 3 and
the symbol for 100, 400 is represented by the symbol for 4 and the symbol for
100, etc. Similarly 2000 is represented by the symbol for 2 and the symbol for
1000, 3000 is represented by the symbol for 3 and the symbol for 1000, 4000 is
represented by the symbol for 4 and the symbol for 1000, etc. There was also a
symbol for 10000 which we have not included in the illustration above but it
took the form of a scorpion. However larger numbers have not been found, the
largest number discovered on the Shang bones and tortoise shells being 30000.
The
additive nature of the system was that symbols were juxtaposed to indicate
addition, so that 4359 was represented by the symbol for 4000 followed by the
symbol for 300, followed by the symbol of 50 followed by the symbol for 9. Here
is the way 4359 would appear: ![]()
Now
this system is not a positional system so it had no need for a zero. For
example the number 5080 is represented by: ![]()
Because
we have not illustrated many numbers above here is one further example of a
Chinese oracular number. Here is 8873: ![]()
There
are a number of fascinating questions which we can consider about this number
system. Although the representation of the numbers 1, 2, 3, 4 needs little
explanation, the question as to why particular symbols are used for the other
digits is far less obvious. Two main theories have been put forward.
The
first theory suggests that the symbols are phonetic. By this we mean that since
the number nine looks like a fish hook, then perhaps the sound of the word for
'nine' in ancient Chinese was close to the sound of the word for 'fish hook'.
Again the symbol for 1000 is a 'man' so perhaps the word for 'thousand' in
ancient Chinese was close to the sound of the word for 'man'. To take an
example from English, the number 10 is pronounced 'ten'. This sounds like 'hen'
so a symbol for a hen might be appropriate, perhaps modified so that the reader
knew that the symbol represented 'ten' rather than 'hen'.
A
second theory about the symbols comes from the fact that numbers, and in fact
all writing in this Late Shang period, were only used as part of religious
ceremonies. We have explained above how the inscriptions were used by
soothsayers, who were the priests of the time, in their ceremonies. This theory
suggests that the number symbols are of religious significance. Of course it is
possible that some of the symbols are explained by the first of these theories,
while others are explained by the second. Again symbols such as the scorpion
may simply have been used since swarms of scorpions meant "a large number'
to people at that time. Perhaps the symbol for 100 represents a toe (it does
look like one), and one might explain this if people at the time counted up to
ten on their fingers, then 100 for each toe, and then 1000 for the 'man' having
counted 'all' parts of the body.
The
symbols we have illustrated evolved somewhat over time but were surprisingly
stable in form. However a second form of Chinese numerals began to be used from
the 4th century BC when counting boards came into use. A counting
board consisted of a checker board with rows and columns. Numbers were
represented by little rods made from bamboo or ivory. A number was formed in a
row with the units placed in the right most column, the tens in the next column
to the left, the hundreds in the next column to the left etc. The most
significant property of representing numbers this way on the counting board was
that it was a natural place valued system. One in the right most column
represented 1, while one in the adjacent column to the left represented 10 etc.
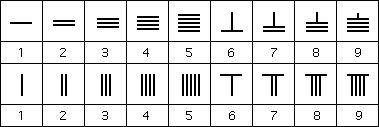
Now the numbers from 1 to 9 had to be formed from the rods and a fairly natural
way was found.
Here
are two possible representations:
The biggest problem with this notation was that it could lead to possible
confusion. What was ||| ? It could be 3, or 21, or 12, or even 111. Rods moving
slightly along the row, or not being placed centrally in the squares, would
lead to the incorrect number being represented. The Chinese adopted a clever
way to avoid this problem. They used both forms of the numbers given in the
above illustration. In the units column they used the form in the lower row,
while in the tens column they used the form in the upper row, continuing
alternately. For example 1234 is represented on the counting board by: ![]() and
45698 by:
and
45698 by: ![]()
There
was still no need for a zero on the counting board for a square was simply left
blank. The alternating forms of the numbers again helped to show that there was
indeed a space. For example 60390 would be represented as: ![]()
Ancient
arithmetic texts described how to perform arithmetic operations on the counting
board. For example Sun Zi, in the first chapter of the Sunzi suanjing
(Sun Zi's Mathematical Manual), gives instructions on using counting rods to
multiply, divide, and compute square roots.
Xiahou
Yang's Xiahou Yang suanjing (Xiahou Yang's Mathematical Manual) written
in the 5th century AD notes that to multiply a number by 10, 100,
1000, or 10000 all that needs to be done is that the rods on the counting board
are moved to the left by 1, 2, 3, or 4 squares. Similarly to divide by 10, 100,
1000, or 10000 the rods are moved to the right by 1, 2, 3, or 4 squares. What
is significant here is that Xiahou Yang seems to understand not only positive
powers of 10 but also decimal fractions as negative powers of 10. This
illustrates the significance of using counting board numerals.
Now
the Chinese counting board numbers were not just used on a counting board,
although this is clearly their origin. They were used in written texts,
particularly mathematical texts, and the power of the place valued notation led
to the Chinese making significant advances. In particular the "tian
yuan" or "coefficient array method" or "method of the
celestial unknown" developed out of the counting board representation of
numbers. This was a notation for an equation and Li Zhi gives the earliest source
of the method, although it must have been invented before his time.
In
about the fourteenth century AD the abacus came into use in China. Certainly
this, like the counting board, seems to have been a Chinese invention. In many
ways it was similar to the counting board, except instead of using rods to
represent numbers, they were represented by beads sliding on a wire.
Arithmetical rules for the abacus were analogous to those of the counting board
(even square roots and cube roots of numbers could be calculated) but it
appears that the abacus was used almost exclusively by merchants who only used
the operations of addition and subtraction.
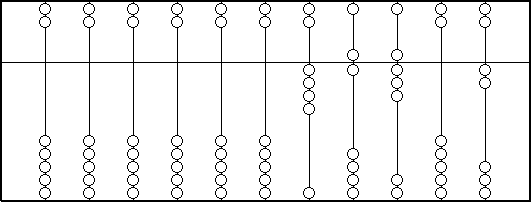
Here is an illustration of an abacus showing the number 46802.
For numbers up to 4 slide the required number of beads in the lower part up to
the middle bar. For example on the right most wire two is represented. For five
or above, slide one bead above the middle bar down (representing 5), and 1, 2,
3 or 4 beads up to the middle bar for the numbers 6, 7, 8, or 9 respectively.
For example on the wire three from the right hand side the number 8 is
represented (5 for the bead above, three beads below).
One
might reasonably ask why each wire contains enough beads to represent 15. This
was to make the intermediate working easier so that in fact numbers bigger than
9 could be stored on a single wire during a calculation, although by the end
such "carries" would have to be taken over to the wire to the left.
Article
by: J J O'Connor
and E F Robertson
January 2004
MacTutor
History of Mathematics
[http://www-history.mcs.st-andrews.ac.uk/HistTopics/Chinese_numerals.html]
History topic: Chinese
problems
We
give here a collection of Chinese problems which are extracted from various
articles in our archive on Chinese mathematics or Chinese mathematicians. Many
of the problems have answers given in the corresponding article, and some have
a description of the method. Each problem has a reference to the article in
which it occurs.
Problem
1: See Nine Chapters
A
good runner can go 100
paces while a poor runner covers 60 paces. The poor runner has covered a
distance of 100 paces before the good runner sets off in pursuit. How
many paces does it take the good runner before he catches up the poor runner.
Problem
2: See Cheng Dawei
Boy
shepherd B with his one sheep behind him asked shepherd A "Are there 100 sheep in your flock?".
Shepherd A replies "Yet add the same flock, the same flock again, half,
one quarter flock and your sheep. There are then 100 sheep
altogether." How many sheep is in shepherd A's flock?
Problem
3: See Yang Hui
Now
1 cubic cun of jade
weighs 7 liang, and 1 cubic cun of rock weighs 6 liang.
Now there is a cube of side 3 cun consisting of a mixture of jade and
rock which weighs 11 jin. Tell: what are the weights of jade and rock in
the cube. [Note 1 jin = 16 liang]
Problem
4: See Sun Zi
Suppose
that, after going through a town gate, you see 9 dykes, with 9 trees on each
dyke, 9 branches on each tree, 9 nests on each branch, and 9
birds in each nest, where each bird has 9 fledglings and each fledgling has 9
feathers with 9 different colours in each feather. How many are there of
each?
Problem
5: See Nine Chapters
Certain
items are purchased jointly. If each person pays 8 coins, the surplus is 3
coins, and if each person gives 7 coins, the deficiency is 4
coins. Find the number of people and the total cost of the items.
Problem
6: See Nine Chapters
There
are two piles, one containing 9
gold coins and the other 11 silver coins. The two piles of coins weigh
the same. One coin is taken from each pile and put into the other. It is now
found that the pile of mainly gold coins weighs 13 units less than the
pile of mainly silver coins. Find the weight of a silver coin and of a gold
coin.
Problem
7: See Nine Chapters
There
is a square town of unknown dimensions. There is a gate in the middle of each
side. Twenty paces outside the North Gate is a tree. If one leaves the town by
the South Gate, walks 14
paces due south, then walks due west for 1775 paces, the tree will just
come into view. What are the dimensions of the town.
Problem
8: See Sun Zi
Suppose
we have an unknown number of objects. When counted in threes, 2 are left over, when counted in
fives, 3 are left over, and when counted in sevens, 2 are left
over. How many objects are there?
Problem
9: See Nine Chapters
A
cistern is filled through five canals. Open the first canal and the cistern
fills in 1/3 day; with the second, it
fills in 1 day; with the third, in 21/2
days; with the fourth, in 3 days, and with the fifth in 5 days. If
all the canals are opened, how long will it take to fill the cistern?
Problem
10: See Li Zhi
Given
a circular walled city of unknown diameter with four gates, one at each of the
four cardinal points. Two persons A and B start from the west gate. B walks a
distance of 256 pu
eastwards. Then A walks a distance of 480 pu south before he can see B.
Find the diameter of the town.
Problem
11: See Li Zhi
Given
a circular walled city of unknown diameter with four gates, one at each of the
four cardinal points. Person A leaves the west gate and walks south for 480 pu. B leaves the east gate and
walks straight ahead a distance of 16 pu, when he just sees A. Find the
diameter of the town.
Problem
12: See Li Zhi
Given
a circular walled city of unknown diameter with four gates, one at each of the
four cardinal points. 135
pu directly out of the south gate is a tree. If one walks 15 pu out of
the north gate and then turns east for a distance of 208 pu, the tree
comes into sight. Find the diameter of the town.
Problem
13: See Qin Jiushao
Given
a circular walled city of unknown diameter with four gates, one at each of the
four cardinal points. A tree lies three li north of the northern gate. If one
turns and walks eastwards for nine li immediately on leaving the southern gate,
the tree just comes into view. Find the circumference and the diameter of the
city wall.
Problem
14: See Li Zhi
A
square farm has a circular pond in the centre. The land area is 13 mou and 71/2
tenths of a mou. The pond is 20 pu from the edge. Find the length of the
side of the farm and the diameter of the pond.
Problem
15: See Cheng Dawei
Now
a pile of rice is against the wall with a base circumference 60 chi and an altitude of 12
chi. What is the volume? Another pile is at an inner corner, with a base
circumference of 30 chi and an altitude of 12 chi. What is the
volume? Another pile is at an outer corner, with base circumference of 90
chi and an altitude of 12 chi. What is the volume?
Problem
16: See Cheng Dawei
A
small river cuts right across a circular field whose area is unknown. Given the
diameter of the field and the breadth of the river find the area of the
non-flooded part of the field.
Problem
17: See Cheng Dawei
In
the right-angled triangle with sides of length a, b and c with a > b > c,
we know that a + b = 81
ken and a + c = 72 ken. Find a, b, and c.
Problem
18: See Zhu Shijie
A
right-angled triangle has area 30
bu. The sum of the base and height of the triangle is 17 bu. What is the
sum of the base and hypotenuse?
Problem
19: See Wang Xiaotong
Let
a right angled triangle have sides a, b, c where c is the hypotenuse. If a
times b is seven hundred and six and one fiftieth, and if c is thirty six and
nine tenths more than a. What are the values of the three sides.
Problem
20: See Zhang Qiujian
A
circular road around a hill is 325
li long. Three persons A, B, and C run along the road. A runs 150 li per
day, B runs 120 li per day, and C runs 90 li per day. If they start at
the same time from the same place, after how many days will they meet again.
Problem
21: See Zhang Qiujian
There
are three persons, A, B, and C each with a number of coins. A says "If I
take 2/3 of B's coins and 1/3
of C's coins then I hold 100". B says If I take 2/3
of A's coins and 1/2 of C's coins then I hold 100
coins". C says "If I take 2/3 of A's
coins and 2/3 of B's coins, then I hold 100
coins". Tell me how many coins do A, B, and C hold?
Problem
22: See Zhang Qiujian
Cockerels
costs 5 qian each,
hens 3 qian each and three chickens cost 1 qian. If 100
fowls are bought for 100 qian, how many cockerels, hens and chickens are
there?
Problem
23: See Yang Hui
100
coins buy Wenzhou oranges, green oranges, and golden oranges, 100 in
total. If a Wenzhou orange costs 7 coins, a green orange 3 coins,
and 3 golden oranges cost 1 coin, how many oranges of the three
kinds will be bought?
Problem
24: See Yang Hui
A
number of pheasants and rabbits are placed together in the same cage.
Thirty-five heads and ninety-four feet are counted. Find the number of pheasants
and rabbits.
Problem
25: See Zhu Shijie
Given
the relations 2yz
= z2 + xz and 2x + 4y + 4z = x(y2
- z + x) between the sides of a right angled triangle x, y, z
where z is the hypotenuse, find d = 2x + 2y.
Problem
26: See Zhu Shijie
If
the cube law is applied to the rate of recruiting soldiers and it is found that
on the first day 3
cubed are recruited, 4 cubed on the second day, and on each succeeding
day the cube of a number one greater than the previous day are recruited, how
many soldiers in total will have been recruited after 15 days? How many
after n days?
Problem
27: See Zhu Shijie
Let
d be the diameter of the circle inscribed in a right triangle (you should use
the relation d = x
+ y - z where x, y, z are as defined below). Let x, y be the lengths
of the two legs and z the length of the hypotenuse of the triangle. Given that
dxy = 24 and x + z = 9 find y.
Article
by: J J O'Connor
and E F Robertson
December 2003
MacTutor
History of Mathematics
[http://www-history.mcs.st-andrews.ac.uk/HistTopics/Chinese_problems.html]