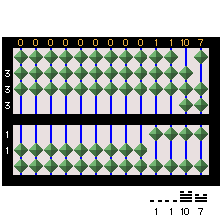
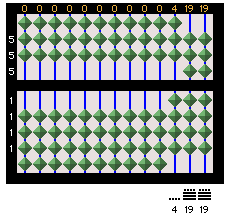
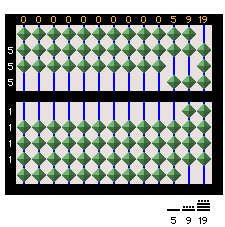
March 2, 2005
A
Brief History of the Abacus
By: Frank J. Collazo
Abacus is a Latin word that has its origins in the Greek
words abax or abakon (meaning “table” or “tablet”) which in turn possibly
originated from the Semitic word abq, meaning “sand.”
Why does the abacus exist?
It is
difficult to imagine counting without numbers, but there was a time when
written numbers did not exist. The earliest counting device was the human
hand and its fingers. Then, as larger
quantities (larger than ten human-fingers could represent) were counted,
various natural items like pebbles and twigs were used to help count. Merchants who traded goods not only needed a
way to count goods they bought and sold, but also to calculate the cost of
those goods. Until numbers were
invented, counting devices were used to make everyday calculations.
What are the difference’s between a counting board
and an abacus?
It is important to distinguish the early abacuses (or abaci) known as counting boards from the modern abaci. The counting board is a piece of wood, stone or metal with carved grooves or painted lines between which beads, pebbles or metal discs were moved. The abacus is a device, usually of wood (plastic, in recent times), having a frame that holds rods with freely sliding beads mounted on them. Both the abacus and the counting board are mechanical aids used for counting; they are not calculators in the sense we use the word today. The person operating the abacus performs calculations in their head and uses the abacus as a physical aid to keep track of the sums, the carrys, etc.
What did the first counting board look like?
The earliest counting boards are forever lost because of
the perishable materials used in their construction. However, educated guesses can be made about their construction,
based on early writings of Plutarch (a priest at the Oracle at Delphi) and
others. In outdoor markets of those
times, the simplest counting board involved drawing lines in the sand with
fingers or a stylus, and placing pebbles between those lines as place-holders
representing numbers (the spaces between 2 lines would represent the units 10s,
100s, etc.). The more affluent could
afford small wooden tables having raised borders that were filled with sand
(usually coloured blue or green).
Another benefit of these counting boards on tables was that they could
be moved without disturbing the calculation and they could also be used
indoors. With the need for something
more durable and portable, wooden boards with grooves carved into them, were
then created and wooden markers (small discs) were used as place-holders. The wooden boards then gave way to even more
more permanent materials like marble and metal with stone and metal markers.
The Salamis Tablet: The oldest counting board, made of
marble, has a large crack across the middle.
Photo from the National Museum of Epigraphy, Athens. The Salamis Tablet is the oldest surviving
counting board (originally thought to be a gaming board), used by the
Babylonians circa 300 B.C., discovered in 1846 on the island of Salamis. It is a slab of white marble measuring 149cm
in length, 75cm in width and 4.5cm thick, on which are 5 groups of
markings. In the center of the tablet
are a set of 5 parallel lines equally divided by a vertical line, capped with a
semi-circle at the intersection of the bottom-most horizontal line and the
single vertical line. Below these lines
is a wide space with a horizontal crack dividing it. Below this crack is another group of eleven parallel lines, again
divided into two sections by a line perpendicular to them but with the
semi-circle at the top of the intersection; the third, sixth and ninth of these
lines are marked with a cross where they intersect with the vertical line. Three sets of Greek symbols (numbers from
the acrophonic system)
are arranged along the left, right and bottom edges of the tablet.
Evolution, The Abacus Through the Ages: The evolution of the abacus can be divided into three ages:
Ancient Times, Middle Ages, and Modern Times.
The time-line below traces the developing abacus from its beginnings
circa 500 B.C., to the present.

Evolutionary Time-line: This
time-line shows the evolution from the earliest counting board to the present
day abacus. (Compared to the rate of
progress in the last one-thousand years, the progress during the first
one-thousand years of civilization was rather slow.)
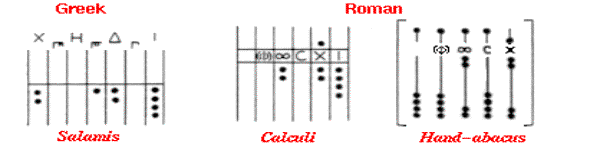
Ancient Times: The Salamis Tablet,
the Roman Calculi and Hand-abacus are from the period c. 300 B.C to c. 500 A.D. During Greek and Roman times, counting
boards, like the Roman hand-abacus,
that survived are constructed from stone and metal (as a point of reference,
the Roman empire fell circa 500 A.D.).

Middle Ages: The Apices, the
coin-board and the Line-board are from the period c. 5 A.D. to c. 1400 A.D. Wood was the primary material from which counting
boards were manufactured; the orientation of the beads switched from vertical
to horizontal. As arithmetic (counting
using written numbers) gained popularity in the latter part of the Middle Ages,
the use of the abacus began to diminish in Europe.
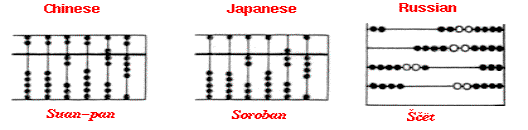
Modern Times: The Suan-pan, the
Soroban and the Schoty are from the period c. 1200 A.D to the present. The abacus as we know it today, appeared
circa 1200 A.D. in China; in Chinese, it is called suan-pan. On each
rod, this classic Chinese abacus has 2 beads on the upper deck and 5 on the
lower deck; such an abacus is also referred to as a 2/5 abacus. The 2/5 style survived unchanged until about
1850 at which time the 1/5 (one bead on the top deck and five beads on the
bottom deck) abacus appeared.
Circa 1600 A.D., use and evolution of the Chinese 1/5
abacus was begun by the Japanese via Korea.
In Japanese, the abacus is called soroban. The ¼ abacus, a style preferred and still
manufactured in Japan today, appeared circa 1930. The 1/5 models are rare today and 2/5 models are rare outside of
China (excepting Chinese communities in North America and elsewhere). It is thought that early Christians brought
the abacus to the East (note that both the suan-pan and the Roman
hand-abacus have a vertical orientation).
There have been recent suggestions of a Mesoamerican (the
Aztec civilization that
existed in present day Mexico) abacus called the Nepohualtzitzin,
circa 900-1000 A.D., where the counters were made from kernels of maize
threaded through strings mounted on a wooden frame. There is also debate about the Incan Khipu—
was it a three-dimensional binary calculator or a form of writing? (q.v. Talking Knots of
the Incas).
The schoty,
is a Russian abacus invented in the 17th century and is still used
today in some parts.
The Lee Kai-chen
Abacus: Further refinement of the Chinese abacus c. 1958.
The Abacus Today:
The image above is a cover of a manual
published in 1958 by Lee Kai-chen, the inventor of this “new” abacus designed
with 4 decks (essentially, it consists of 2 stacked abaci; the top abacus is a
small ¼ soroban and the bottom one is a 2/5 suan-pan). The author claims that multiplication and
division are easier using this modified abacus and includes instructions for
determining square roots and cubic roots of numbers.
In the history of mathematics, the contributions of the
Roman Empire are sometimes overlooked. Roman Numerals are
considered cumbersome and the Roman’s lack of contributions to mathematics, and
the lack of the Zero, are held in low esteem.
And yet, the Roman Empire was likely the largest when viewed as a
percent of world population. Their
empire consistently built engineering marvels: roads that survive and are used
to this day, homes and bath houses with indirect heating emulated today,
plumbed sewer and water lines in and out of homes and public buildings, indoor
toilets, aquaducts that included long tunnels and bridges, and huge, beautiful
buildings. Their engineers and
architects designed and built these using counting boards and hand abaci; using
Roman Numerals only to record the results.
Roman Hand-Abacus:
A photocopy of a photograph of the Roman hand-abacus; the top image is
the front and the bottom is the back.
Image is from Museo Nazionale Ramano at Piazzi delle Terme, Rome. The longevity of their empire was due to
their commercial trade—they were businessmen.
The intricate, complex, and extensive accounting of their trade was
conducted with counting boards and hand-abaci; again using Roman Numerals only
to record the results and as anyone knows who has used a counting board or
abacus, your rows or columns often represent nothing, or zero. Since the Romans used Roman Numerals to
record results, and since Roman Numerals were positively definitive, there was
no need for a zero notation, but the Romans certainly knew the concept of zero
occuring in any place value, row or column.
One could also infer that they were aware of the concept of a negative
number. How else would Roman merchants
understand and manipulate liabilities against assets and loans versus
investments? The Romans developed their
hand-abacus as a portable counting board—the first portable calculating device
for both engineers and businessmen.
The Roman Hand-Abacus by Steve Stephenson: In the history of mathematics, the contributions of the Roman
Empire are sometimes overlooked. Roman Numerals are
considered cumbersome and the Roman’s lack of contributions to mathematics, and
the lack of the Zero, are held in low esteem.
And yet, the Roman Empire was likely the largest when viewed as a percent
of world population. Their empire
consistently built engineering marvels: roads that survive and are used to this
day, homes and bath houses with indirect heating emulated today, plumbed sewer
and water lines in and out of homes and public buildings, indoor toilets,
aquaducts that included long tunnels and bridges, and huge, beautiful
buildings. Their engineers and
architects designed and built these using counting boards and hand abaci; using
Roman Numerals only to record the results.
Layout of the Roman Hand-Abacus: Here’s the London Science Museum’s Roman hand-abacus
layout, where the ~3 was actually a symbol that
looked like a 3 that was flattened on the top then flipped top to bottom and
right to left, or rotated 180 degrees:
| | | |
| | | | | | | |
| | | |
| | | |
| | | | | |
| | | | | |
|*| |*|
|*| |*| |*|
|*| |*| |*|
|X| (((|))) ((|)) (|) C X
I 0 ~3
| | | |
| | | | | |
| | | | | |
| |
| | | |
| | | | | |
| | | | | |
| | )
|*| |*|
|*| |*| |*|
|*| |*| |*|
| |
|*| |*|
|*| |*| |*|
|*| |*| |*|
| |
|*| |*|
|*| |*| |*|
|*| |*| |*|
| |
|*| |*|
|*| |*| |*|
|*| |*| |*|
|*| 2
|*| |*|
Figure
16.94
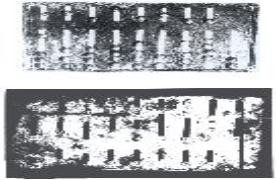
Roman “pocket abacus”: In bronze, beginning of Common Era
(Cabinet des Médailles, Bibliothèque nationale, Paris). Note that Figure 16.94 has beads missing
from most of the slots. The drawing on
the bottom has incorrectly labeled the right-most slot. This abacus is similar to the one being
described in this article. Image and caption from, The Universal History of
Numbers, Georges Ifrah, Wiley Press 2000. (Click to enlarge.)
The abacus was made of a metal plate where the beads ran in slots. The size was such that the abacus could fit
in a modern shirt pocket. The upper
slots contained a single bead while the lower slots contained 4 beads, the only
exceptions being the two right-most columns, marked 0 and ~3. (Note the longer slots below the 0 and ~3
positions, the 5 beads in the lower slot of the 0 position, the 2 beads in the
lower slot of the ~3 position, and the absence of an upper slot in the ~3 position,
I wonder what the ‘)’ and ‘2’ symbols along the right side of the ~3 slot
meant?) Obviously
the units in the 0 position were 1/12 of the I position, and the units in the
~3 position were 1/3 of the 0 position.
So the upside down reversed 3 character seems appropriate to represent
1/3; or, more likely, our symbol for 3 came from the Roman symbol for 1/3.
It is also worth noting that:
The Roman hand-abacus predates the Chinese “invention” of
the Suan Pan.
The Romans traded with the Chinese over the Silk Road
(did the Chinese copy the Romans’ hand-abacus?)
The Roman hand-abacus has the refinements attributed to
the modern Japanese Soroban; i.e. one bead above and four
beads below the bar (did the Japanese copy the Romans’ hand-abacus instead of the
Chinese Suan Pan?)
The Roman hand-abacus incorporates mixed base arithmetic
(in the two rightmost columns), another original enhancement by the Romans that
is not present in any other abacus.
A Possible Time Abacus: The last point, above, might lead one to develop a Time abacus.
|*| |*| |*|
|*|
|*| |*| |*|
|*| |*| |*|
| |
| | | | | |
| | | | | |
| |
| | | | | |
| | | | | |
y q
w d 6h h 6m
m 6s s s/10
| | | | | |
| | | | | |
| | | | | |
| | | |
| | | | | |
| | | | | |
| | | | | |
| | | |
|*| |*| |*|
|*| |*| |*|
|*| |*| |*|
|*| |*|
|*| |*| |*|
|*| |*| |*| |*| |*|
|*| |*| |*|
|*| |*| |*| |*| |*|
|*| |*| |*| |*|
|*| |*|
|*| |*|
|*| |*|
|*|
|*|
|*|
|*|
|*|
|*|
|
|
|
|
|
Description |
Base |
|
|
y |
year |
10 |
|
q |
quarter |
4 |
|
w |
week |
13 |
|
d |
day |
7 |
|
6h |
six hours = ¼ day |
4 |
|
h |
hour |
6 |
|
6m |
six minutes = 1/10 hour |
10 |
|
m |
minute |
6 |
|
6s |
six seconds = 1/10 minute |
10 |
|
s |
second |
6 |
|
s/10 |
1/10 second |
10 |
The quarters and years calculate an exact 364 day year,
not the (currently) correct 365.242190 day year.
|
Handy
Roman numeral converter Top of
Form Bottom
of Form Script courtesy |
The Romans
were active in trade and commerce, and from the time of learning to write they
needed a way to indicate numbers. The
system they developed lasted many centuries, and still sees some specialized
use today.
Roman
numerals traditionally indicate the order of rulers or ships that share the
same name (i.e. Queen Elizabeth II).
They are also sometimes still used in the publishing industry for
copyright dates, and on cornerstones and gravestones when the owner of a
building or the family of the deceased wishes to create an impression of
classical dignity. The Roman numbering
system also lives on in our languages, which still use Latin word roots to
express numerical ideas. A few
examples: unilateral, duo, quadriceps, septuagenarian, decade, and
milliliter. The big differences between
Roman and Arabic numerals (the ones we use today) are that Romans didn’t have a
symbol for zero, and that numeral placements within a number can sometimes
indicate subtraction rather than addition.
Here are the basics:
|
I |
The
easiest way to note down a number is to make that many marks - little I’s.
Thus I means 1, II means 2, III means 3. However, four strokes seemed like
too many.... |
|
V |
So the
Romans moved on to the symbol for 5 - V. Placing I in front of the V — or
placing any smaller number in front of any larger number — indicates
subtraction. So IV means 4. After V comes a series of additions - VI means 6,
VII means 7, VIII means 8. |
|
X |
X means
10. But wait — what about 9? Same deal. IX means to subtract I from X,
leaving 9. Numbers in the teens, twenties and thirties follow the same form
as the first set, only with X’s indicating the number of tens. So XXXI is 31,
and XXIV is 24. |
|
L |
L means
50. Based on what you’ve learned, I bet you can figure out what 40 is. If you
guessed XL, you’re right = 10 subtracted from 50. And thus 60, 70, and 80 are
LX, LXX and LXXX. |
|
C |
C
stands for centum, the Latin word for 100. A centurion led 100
men. We still use this in words like “century” and “cent.” The subtraction
rule means 90 is written as XC. Like the X’s and L’s, the C’s are tacked on
to the beginning of numbers to indicate how many hundreds there are: CCCLXIX
is 369. |
|
D |
D
stands for 500. As you can probably guess by this time, CD means 400. So
CDXLVIII is 448. (See why we switched systems?) |
|
M |
M is
1,000. You see a lot of Ms because Roman numerals are used a lot to indicate
dates. For instance, this page was written in the year of Nova Roma’s
founding, 1998 CE (Common Era; Christians use AD for Anno Domini, “year of
our Lord”). That year is written as MCMXCVIII. But wait! Nova Roma counts
years from the founding of Rome, ab urbe condita. By that reckoning
this is 2751, or MMDCCLI. |
The Abacus vs. the Electric Calculator:
Excerpted from the book, “The Japanese Abacus, Its Use and Theory,” by Takashi
Kojima, Charles E. Tuttle Company Inc. 1954, reprint 1987. ISBN: 0-8048-0278-5.
The abacus, or soroban as it is called in Japan, is one
of the first objects that strongly attracts the attention of the foreigner in
Japan. When he buys a few trifling
articles at some store, he soon notices that the tradesman does not perplex
himself with mental arithmetic, but instead seizes his soroban, prepare it by a
tilt and a rattling sweep of his hand, and after a deft manipulation of rapid
clicks, reads off the price. It is true
that the Japanese tradesman often uses his board and beads even when the
problem is simple enough to be done in one’s head, but this is only because the
use of the abacus has become a habit with him.
If he tried, he could no doubt easily add 37 and 48 in his head. But such is the force of habit that he does
not try to recognize the simplicity of any problem; instead, following the line
of least resistance, he adjusts his soroban for manipulation, and begins
clicking the beads, thus escaping any need of mental effort.
Doubtlessly the Westerner, with his
belief in the powers of mental arithmetic and the modern calculating machine,
often mistrusts the efficiency of such a primitive looking instrument. However, his mistrust of the soroban is
likely to be transformed into admiration when he gains some knowledge
concerning it. For the soroban, which
can perform in a fraction of time, a difficult arithmetic calculation that the
Westerner could do laboriously only by means of pencil and paper, possesses
distinct advantages over mental and written arithmetic. The Japanese tradesman with his soroban
would easily outstrip a rapid and accurate Western accountant even with his
adding machine. An exciting contest
between the Japanese abacus and the electric calculating machine was held in
Tokyo on November 12, 1946, under the sponsorship of the U. S. Army newspaper,
the Stars and Stripes. In reporting
the contest, the Stars and Stripes remarked:
“The machine age tool took a step
backward yesterday at the Emie Pyle Theater as the abacus, centuries old, dealt
defeat to the most up-to-date electric machine now being used by the United
States Government...The abacus victory was decisive.”
The Nippon Times reported the
contest as follows: “Civilization, on the threshold of the atomic age,
tottered Monday afternoon as the 2,000-year-old abacus beat the electric
calculating machine in adding, subtracting, dividing and a problem including
all three with multiplication thrown in, according to UP. Only in
multiplication alone did the machine triumph...”
The American representative of the calculating machine was Pvt. Thomas
Nathan Wood of the 20th Finance Disbursing Section of General
MacArthur’s headquarters, who had been selected in an arithmetic contest as the
most expert operator of the electric calculator in Japan. The Japanese
representative was Mr. Kiyoshi Matsuzaki, a champion operator of the abacus in
the Savings Bureau of the Ministry of Postal Administration.
As may be seen from the results
tabulated below, the abacus scored a total of 4 points as against 1 point for
the electric calculator. Such results
should convince even the most skeptical that, at least so far as addition and
subtraction are concerned, the abacus possesses an indisputable advantage over
the calculating machine. Its advantages
in the fields of multiplication and division, however, were not so decisively
demonstrated.
|
Type of Problem |
Name |
1st Heat |
2nd Heat |
3rd Heat |
Score |
|
Addition: 50 numbers each containing 3 to 6 digits |
Matsuzaki |
1m. 14.9s |
1m 16s |
|
1 |
|
Wood |
2m 0.2s |
1m 58s |
|
|
|
|
Subtraction: 5 problems with minuends
and subtrahends of from 6 to 8 digits each |
Matsuzaki |
1m .4s |
1m .8s |
1m |
1 |
|
Wood |
1m 30s |
1m 35s |
1m 22s |
|
|
|
Multiplication: 5 problems each
containing 5 to 12 digits in the multiplier and multiplicand |
Matsuzaki |
1m 44.6s |
1m 19s |
2m 14.4s |
|
|
Wood |
2m 22s |
1m 20s |
1m 53.6s |
1 |
|
|
Division: 5 problems each containing 5
to 12 digits in the divisor and dividend |
Matsuzaki |
1m 36.6s |
1m 23s |
1m 21s |
1 |
|
Wood |
1m 48s |
1m 19s |
1m 25s |
|
|
|
Composite problems: 1 problem in
addition 30 6-digit numbers; 3 problems in subtraction, each with two 6-digit
numbers; 8 problems in multiplication each with two figures containing a
total of 5 to 12 digits; 3 problems in division, each with two figures
containing a total of 5 to 12 digits |
Matsuzaki |
1m 21s |
|
|
1 |
|
Wood |
1m 26s |
|
|
|
|
|
Total Score: |
Matsuzaki |
|
|
|
4 |
|
Wood |
|
|
|
1 |
Results of the Contest: Matsuzaki using the abacus, wins 4 to
1 against Wood, using the electric calculator.
This is an excerpt from the chapter “Lucky Numbers”, in Surely, You’re
Joking, Mr. Feynman!, Edward Hutchings ed., W. W. Norton, ISBN: 0-393-31604-1.
The story is taking place in Brazil; the narrator is Richard Feynman. A Japanese man
came into the restaurant. I had seen
him before, wandering around; he was trying to sell abacuses. He started to
talk to the waiters, and challenged them: He said he could add numbers faster
than any of them could do. The
waiters didn’t want to lose face, so they said, “Yeah, yeah. Why don’t you go
over and challenge the customer over there?”
The man came over. I protested,
“But I don’t speak Portuguese well!”
The waiters laughed. “The
numbers are easy” they said. They
brought me a paper and pencil. The man
asked a waiter to call out some numbers to add. He beat me hollow, because while I was writing the numbers down,
he was already adding them as he went along.
I suggested that the waiter write down two identical lists of numbers
and hand them to us at the same time.
It didn’t make much difference.
He still beat me by quite a bit.
However, the man got a little bit
excited: he wanted to prove himself some more. “Multiplicação!” he
said. Somebody wrote down a
problem. He beat me again, but not by
much, because I’m pretty good at products.
The man then made a mistake: he proposed we go on to division. What he didn’t realize was, the harder the
problem, the better chance I had. We
both did a long division problem. It
was a tie.
That bothered the hell out of the
Japanese man, because he was apparently well trained on the abacus, and here he
was almost beaten by this customer in a restaurant. “Raios cubicos!” he says with a vengeance. Cube roots!
He wants to do cube roots by arithmetic. It’s hard to find a more difficult fundamental problem in
arithmetic. It must have been his
topnotch exercise in abacus-land. He
writes down a number on some paper— any old number— and I still remember it:
1729.03. He starts working on it,
mumbling and grumbling: “Mmmmmmagmmmmbrrr”— he’s working like a
demon! He’s poring away, doing this
cube root. Meanwhile I’m just sitting
there. One of the waiters says, “What
are you doing?”. I point to my
head. “Thinking!” I say. I write down 12 on the paper. After a little while I’ve got 12.002. The man with the abacus wipes the sweat off
his forehead: “Twelve!” he says. “Oh,
no!” I say. “More digits! More
digits!” I know that in taking a cube
root by arithmetic, each new digit is even more work that the one before. It’s a hard job. He buries himself again, grunting “Rrrrgrrrrmmmmmm ...,”
while I add on two more digits. He
finally lifts his head to say, “12.01!”
The waiter are all excited and happy.
They tell the man, “Look! He
does it only by thinking, and you need an abacus! He’s got more digits!” He
was completely washed out, and left, humiliated. The waiters congratulated each other. How did the customer beat the abacus? The number was 1729.03.
I happened to know that a cubic foot
contains 1728 cubic inches, so the answer is a tiny bit more than 12. The excess, 1.03 is only one part in nearly
2000, and I had learned in calculus that for small fractions, the cube root’s
excess is one-third of the number’s excess.
So all I had to do is find the fraction 1/1728, and multiply by 4
(divide by 3 and multiply by 12). So I
was able to pull out a whole lot of digits that way.
A few weeks later, the man came into
the cocktail lounge of the hotel I was staying at. He recognized me and came over. “Tell me,” he said, “how were you
able to do that cube-root problem so fast?”
I started to explain that it was an approximate method, and had to do
with the percentage of error. “Suppose
you had given me 28. Now the cube root
of 27 is 3 ...”
He picks up his abacus: zzzzzzzzzzzzzzz—
“Oh yes,” he says. I realized
something: he doesn’t know numbers.
With the abacus, you don’t have to memorize a lot of arithmetic
combinations; all you have to do is to learn to push the little beads up and
down. You don’t have to memorize
9+7=16; you just know that when you add 9, you push a ten’s bead up and pull a
one’s bead down. So we’re slower at basic
arithmetic, but we know numbers.
Furthermore, the whole idea of an
approximate method was beyond him, even though a cubic root often cannot be
computed exactly by any method. So I
never could teach him how I did cube roots or explain how lucky I was that he
happened to choose 1729.03.
A Comparison of the Organization and Use of Chinese and
Mesoamerican Abaci
by David B. Kelley:
The Mesoamerican bar-and-dot number system has
similarities to the Chinese solid-and-broken-bar system.

Bar-and-dot System: The numbers 1 to 9 represented using
the Mesoamerican bar-and-dot system; a dot represents “1” and a bar represents
“5”. The remains of a ¾ vigesimal1
(base twenty number system) abacus were purportedly found in Mexico. Whether or not this is true, the fact
remains that the Mesoamerican bar-and-dot number signs appear to fit very
systematically into such an arrangement, as demonstrated below. Additionally, this arrangement, involving
seven rows and thirteen columns, also matches the most common arrangement for
the Chinese decimal/hexadecimal (base sixteen) abacus is something that cannot
be ignored. The evident similarities in
the design of the Chinese solid-and-broken-bar and the Mesoamerican bar-and-dot
number symbols is suggestive of some sort of relationship between the two
systems. What that relationship may be
is not clear, but it is hoped that further research will reveal its nature.
Terminology:
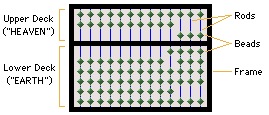
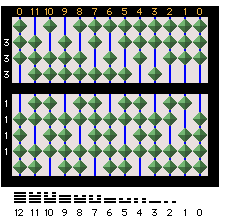
The 2/5 Chinese Abacus: The components of a 2/5
(indicating 2 beads in the Upper Deck and 5 beads in the Lower Deck) Chinese
abacus are identified in this image.
The beads are arranged to show the decimal number 1,999.
The Comparisons:
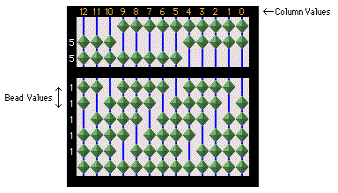
Example Decimal Abacus: The abaci showing simple column
values and bead values appearing in the examples below, display column-values
along the top and and the bead-values on the left.
In the following set of comparisons, the same number is
represented in the left image using the Chinese solid-and-broken-bar system and
in the right image using the Mesoamerican bar-and-dot system.
|
¾ Abacus: simple column values with Chinese solid-and-broken-bar
signs and number values below. This is NOT a functional Duodecimal (base 12)
Abacus, and although each lower deck bead has a value of “1”, each Broken Bar
sign below, actually has a numeric value of “2”. |
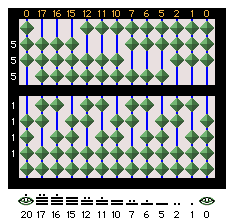
¾ Vigesimal Abacus: simple column values with Mesoamerican
bar-and-dot signs and number values below. This is a fully functional
Vigesimal Abacus, but owing to a 13-column limitation, only 11 bar-and-dot
signs and values, and two uses of the “zero” sign are shown. |
|
3/2 Duodecimal (base 12) Abacus: simple column values with
Chinese solid-and-broken-bar signs and number values below. This is a fully
functional Duodecimal Abacus, and to make it functional, the value of the
Broken Bar sign has been changed to “1”, and the signs and values
re-arranged. |
3/2 Abacus: simple column values with Mesoamerican bar-and-dot
signs and number values below. This is NOT a vigesimal abacus. |
Examples of Place-Value Use:
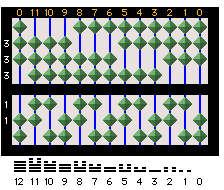
|
3/2 Duodecimal Abacus: place-value column values with Chinese
solid-and-broken-bar signs and number values below showing the decimal number
1,999.
|
¾ Vigesimal Abacus: Regular place-value column values with
Mesoamerican bar-and-dot signs and number values below showing the decimal
number 1,999.
|
|||||||||||||||||||||||||||
|
3/2 Duodecimal Abacus: place-value column values with Chinese
solid-and-broken-bar signs and number values below.
The solid-and-broken-bar signs are markedly similar to the
Mesoamerican bar-and-dot signs, especially those associated with the
Calendric use of the Mesoamerican signs. In the case of the example above, we
see a total of five solid-bar signs and four broken-bar signs each consisting
of two sub-parts, are very similar to the five Mesoamerican bar-signs and
eight dot-signs. |
3/2 Vigesimal Abacus: Calendric place-value column values with
Mesoamerican bar-and-dot signs and number values below.
The abacus shown above has been modified to reflect the
Calendric use of the Mesoamerican vigesimal number system. This means that
the third column has a limit of three upper-deck beads (with each bead = “5”)
and two lower-deck beads ((with each bead = “1”). Accordingly, all columns to
the left of the second column have different values from those derived from
the Regular vigesimal abacus presented earlier. |
|||||||||||||||||||||||||||
Final Comments: The
solid-and-broken-bar (I-Ching) number signs represent one of the
several variant Chinese number-symbol systems.
The Chinese I-Ching number symbols are based on a combination
of the two Yao (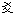 )
‘Elementary Forms’. And, the two Yao
form the basis of the Pa-Kua (
)
‘Elementary Forms’. And, the two Yao
form the basis of the Pa-Kua (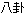 )
‘Eight Diagrams’ found in the I-Ching (
)
‘Eight Diagrams’ found in the I-Ching ( ) ‘Book
of Divination’. On the two Yao,
the I-Ching specifically states that, “The number 3 was assigned to
heaven, 2 to earth, and from these came the (other) numbers.”; the original
line in Chinese is, “
) ‘Book
of Divination’. On the two Yao,
the I-Ching specifically states that, “The number 3 was assigned to
heaven, 2 to earth, and from these came the (other) numbers.”; the original
line in Chinese is, “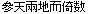 ”2. This has been interpreted to mean that the
Solid-Bar had a numeric value of “3” and the Broken-Bar a value of “2”. However, as the above analyses demonstrate,
with those values the two Yao cannot generate a complete series of numbers,
because there is no sign with a value of “1”.
”2. This has been interpreted to mean that the
Solid-Bar had a numeric value of “3” and the Broken-Bar a value of “2”. However, as the above analyses demonstrate,
with those values the two Yao cannot generate a complete series of numbers,
because there is no sign with a value of “1”.
And so, the pertinent line from the I-Ching was
perhaps mis-interpreted; the line appears to describe an actual 3/2 duodecimal
abacus, and was referring to its two decks: the upper one (“Heaven”) with three
beads per column, and the lower one (“Earth”) with two beads per column. Finally, in order for the duodecimal abacus
to be fully functional, each Upper Deck bead and associated Solid Bar sign
would have necessitated a value of “3”, and each Lower Deck bead and associated
Broken Bar sign, a value of “1”.